Question

Известно, что процент неуспевающих учеников в классе заключен в пределах от 2,3% до 2,9%. Определить минимально возможное количество учеников в классе​

Answer 1

ответ: 35

Объяснение:

Предположим, что в классе  менее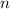 $n$ человек, причем 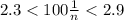$2.3$ ,тогда  минимальный процент неуспевающих учеников будет достигнут при наибольшем возможном числе  учеников, то есть $n-1$ и при минимальном числе неуспевающих учеников, то есть $1$ .

Таким образом, при таком условии процент неуспевающих учеников :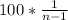 $100*\frac{1}{n-1}$

Найдем минимальное число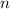 $n$ удовлетворяющее неравенству:

$2.3$

Предположим, что в классе менее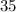 $35$ человек, тогда минимальный процент учеников неуспевающих в классе

$100\frac{1}{34} =\frac{100}{34} = 2+ \frac{32}{34} = 2+ \frac{16}{17}$

Сравним:

$2+\frac{16}{17}$ и  $2.9$

$2+\frac{16}{17}$ и $2+\frac{9}{10}$

$\frac{16}{17}$ и $\frac{9}{10}$

$\frac{160}{170}\frac{153}{170}$  

$100\frac{1}{34} 2.9$

То есть мы пришли к противоречию. А значит в классе как минимум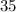 $35$ человек. C другой стороны, как было показано выше, для случая 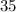$35$ человек может быть достигнут процент неуспевающих учеников в пределах от 2,3% до 2,9%. Это произойдет когда в классе из 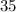$35$ человек неуспевает ровно $1$ ученик.