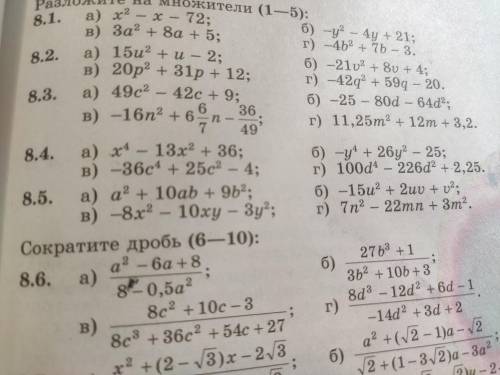
Объяснение:
y=√(x²-16)
подкоренное выражение должно быть≥0
x²-16≥0
(x-4)(x+4)≥0 решим неравенство методом интервалов
для этого приравняем выражение к 0 и найдем корни
(x-4)(x+4)=0
x₁=-4 ; x₂=4 нанесем корни на числовую прямую и определим знак выражения x²-16 на каждом интервале
коэффициент при x² равен 1 и 1>0 значит
по свойству квадратичной функции ветки параболы направлены вверх и знаки на интервалах будут (+)(-)(+)
(-4)4>
+ - +
так как неравенство x²-16≥0 выбираем интервалы со знаком +
x∈(-∞;-4]∪[4;+∞) это область определения функции
или можно записать в следующем виде
D(y)=x∈(-∞;-4]∪[4;+∞)
а) (x-3)(x-2)(x+2)(x+3)
б) (5-y)(y-1)(y+1)(y+5)
в) (2-3c)(2c-1)(2c+1)(3c+2)
г) (5d-0.5)(2d-3)(2d+3)(5d+0.5)
Объяснение:
а)
б)
В первых двух примерах я находил корни квадратных трехчленов на последнем шаге по теореме Виета.
в)
г)