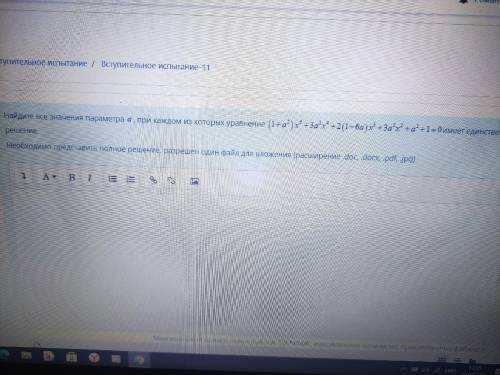
ответ: V1=24 км/ч, V2= 40 км/ч.
Объяснение:
Пусть скорость второго равна х км/ч.
Тогда первого будет х+16 км/ч.
Первый затратит на путь в 120 км - 120/(х+16) часов,
А второй - 120/х часов.
Разность во времени 2 часа.
Составим уравнение:
120/х - 120/(х+16)=2;
Найдем общий знаменатель: х(х+16), дополнительные множители:
(х+16, х и х(х+16)) .
120(х+16)-120х=2х(х+16);
120х+1920-120х=2х²+32х;
2х²+32х-1920=0; [:2]
x²+16x-960=0;
По теореме Виета
х1+х2=-16; х1*х2=960;
х1=24; х2= -40 - не соответствует условию задачи.
V2=24 км/ч - скорость второго мотоциклиста.
V1=x+16=24+16=40 км /ч
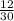 *100% =0,4*100% = 40%
*100% =0,4*100% = 40%
(см. объяснение)
Объяснение:
Заметим, что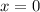 не является корнем уравнения.
не является корнем уравнения.
Тогда поделим его на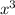 :
:
Выполним группировку:
Заметим, что если - корень уравнения, то
- корень уравнения, то  тоже.
тоже.
Тогда единственное решение возможно, если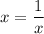 .
.
Иными словами, исходное уравнение может иметь ровно один корень тогда, когда .
.
Подставляя в исходное уравнение, получаем, что
в исходное уравнение, получаем, что 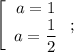
Подставляя , получаем, что
, получаем, что 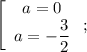
Теперь решим уравнение при каждом найденном значении параметра и отберем те, при которых имеется единственное решение.
Выполнив необходимые вычисления, получаем, что каждое значение параметра подходит.
Итого при исходное уравнение имеет единственное решение.
исходное уравнение имеет единственное решение.
Задание выполнено!