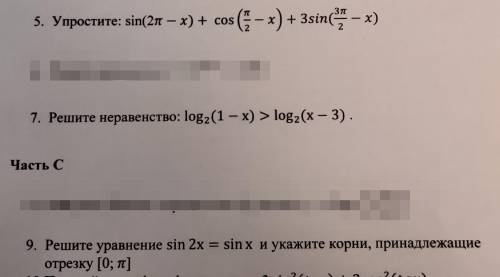

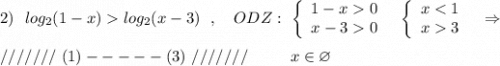
![3)\ \ sin2x=sinx\\\\2\, sinx\cdot cosx-sinx=0\\\\sinx\cdot (2cosx-1)=0\\\\\\a)\ \ sinx=0\ \ \to \ \ \ \boxed{\ x=\pi n\ ,\ n\in Z\ }\\\\\\b)\ \ cosx=\dfrac{1}{2}\ \ \to \ \ \ \boxed{\ x=\pm \dfrac{\pi}{3}+2\pi k\ ,\ k\in Z\ }\\\\\\c)\ \ x\in [\ 0\ ;\ \pi \ ]:\ \ \boxed{\ x_1=0\ ,\ x_2=\dfrac{\pi}{3}\ ,\ x_3=\pi \ }\ .](/tpl/images/2009/5419/ceede.png)
1° = pi/180 радиан ~ 0,017453293 радиан
1° = 1/360 оборота ~ 0,002777 оборота
1° = 400/360 градов ~ 1,111111 градов
Соотношение радиана с другими единицами измерения углов описывается формулой:
* 1 радиан = 1/2π оборотов = 180/π градусов = 200/π градов
Очевидно, 180° = π. Отсюда вытекает тривиальная формула пересчёта из градусов, минут и секунд в радианы и наоборот.
α[рад] = (π / 180) × α[°]
α[°] = (180 / π) × α[рад]
где: α[рад] — угол в радианах, α[°] — угол в градусах
1 рад ≈ 57,295779513° ≈ 57°17′44,806″
Теорема Виета позволяет быстрее решать приведенные квадратные уравнения, не прибегая к объемному решения через дискриминант.
Приведенными квадратными уравнениями называются те квадратные уравнения, в которых коэффициент а=1 (для формулы ax²+bx+c=0)
То есть, общий вид этих уравнений таков: x²+bx+c=0
Согласно теореме, сумма решений уравнения равна противоположному значению коэффициента b, а произведение решений равно коэффициенту с:
x₁+x₂=-b
x₁*x₂=c
Решаются такие уравнения подбором чисел, которые подходили бы под оба условия теоремы. Например:
x²+6x+8=0
x₁+x₂=-6
x₁*x₂=8
Мы видим, что сумма решений отрицательна, значит как минимум одно из решений меньше нуля. В таком случае, произведение тоже было бы отрицательным, но это не так. Значит оба решения меньше нуля. Вспоминаем, какие числа при умножении дают 8:
-1 и -8 не подходит, так как -1+(-8)=-9, а не -6, как нужно нам
-2 и -4 подходит, так как -2+(-4)=-6, а -2*(-4)=8
Следовательно, решениями являются числа -2 и -6, так как соответствуют обоим условиям теоремы.