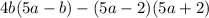

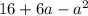

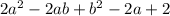
обозначим ширину прямоугольника-x дм, длина будет-(x+4)дм.площадь квадрата с стороной, равной ширине прямоугольника ,будет S=x^2 ,у нас таких 2.
площадь квадрата с стороной, равной длине прямоугольника ,будет S=(x+4)^2
у нас таикх тоже два. Как известно,сумма площадей четырех квадратов, построенных на сторонах прямоугольника, равна 52 дм^2
итого получим уровнение:
2x^2+2(x+4)^2=52
2x^2+2(x^2+8x+16)=52
2x^2+2x^2+16x+32=52
4x^2+16x-20=0
x^2+4x-5=0
решаем квадратное уровнение
D/4=4+5=9
x1=-2+3=1
x2=-2-3=-5 это значение не подойдет оно отрицательное
x=1
x+4=1+4=5
ответ:ширина -1дм; длина- 5дм
а) 4 при a = 2k, b = 5k; 4 при a = b = 2; 25 при a = 3;
б) 1 при a = 3; 1 при a = b = 1
Объяснение:
а)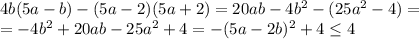
Наибольшее значение (4) достигается, когда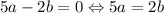 , то есть подходят все пары вида a = 2k, b = 5k. Например, максимальное значение достигается при a = 2, b = 5.
, то есть подходят все пары вида a = 2k, b = 5k. Например, максимальное значение достигается при a = 2, b = 5.
Наибольшее значение (4) достигается, когда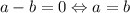 и
и 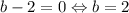 , то есть при a = b = 2.
, то есть при a = b = 2.
Наибольшее значение (25) достигается, когда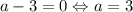 .
.
б)
Наименьшее значение (1) достигается при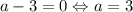
Наименьшее значение (1) достигается, когда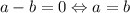 и
и  , то есть при a = b = 1.
, то есть при a = b = 1.