Question

√1+x^4=1/x корень касается и x^4 сколько корней имеет уравнение

Answer 1

Один  корень

Объяснение:

Левая часть -  положительна , значит положительна и правая ,  

  то есть x > 0  ,   но  тогда функция , стоящая в левой части - возрастает

( как сложная  функция , составленная  их двух  возрастающих )  , а  в

правой части - убывающая функция , значит уравнение может иметь не

более одного корня  ;  

Функция y =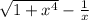 $\sqrt{1 +x^{4} } - \frac{1}{x}$    непрерывна  при x > 0  ;          

 y ( 0,1 ) =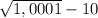 $\sqrt{1,0001} - 10$ <  0  ;   y (1) =  $\sqrt{2} -1 0$  ⇒    

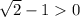на интервале ( 0 ; 1 )   y (x)   имеет корень  и как доказано  он

 единственный