log(4) (x + 2) - log(4) (x + 5) < 1
log(a) b a>0 b>0 a≠1
log(a) b - log(a) c = log(a) b/c
x+2>0 x>-2
x+5>0 x>-5
ОДЗ x∈(-2 +∞)
log(4) (x + 2) - log(4) (x + 5) < 1
log(4) (x + 2) / (x + 5) < log(4) 4
основание больше 1 снимаем логарифмы без изменения знака
(x + 2) / (x + 5) < 4
(x + 2)/(x + 5) - 4 < 0
(x + 2 - 4x - 20)/(x + 5) < 0
(- 3x - 18)/(x + 5) < 0
- 3(x + 6)/(x + 5) < 0
(x+6)/(x+5) > 0
-------------- (-6) ++++++++++ (-5) -------------------
x∈(-∞ -6) U (-5 +∞)
пересекаем с ОДЗ
x∈(-2 +∞)
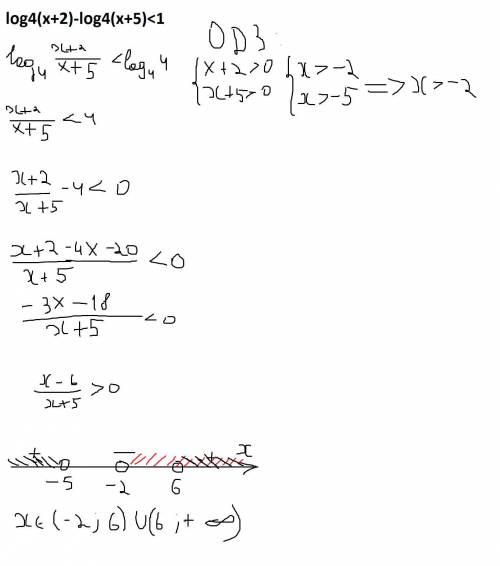
ответ: 8
Объяснение:
Наибольшее значение это соответственно вершина параболы функции y=ax²+bx+c Можно вычислить по формуле :