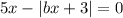 при всех значениях параметра b
при всех значениях параметра b|bx + 3| = 5x
При x ≥ 0 возводим обе части уравнения в квадрат.
|bx + 3|² = (5x)² ⇔ (bx + 3)² = (5x)² ⇒ (bx + 3)² - (5x)² = 0
(bx + 3 - 5x)(bx + 3 + 5x) = 0
bx + 3 - 5x = 0 ⇒ x(b - 5) = -3
Если b = 5, то уравнение, то 0x = -3, уравнение решений не имеет, если b ≠ 5 и то уравнение имеет корень x = 3/(5-b) и причём имеет корень, когда 3/(5-b) ≥ 0 откуда b<5, а при b > 5 не имеет корень
bx + 3 + 5x = 0 ⇒ x(b + 5) = -3
Если b = -5, то -10x = -3 ⇒ x=3/10. Если b ≠ -5, то уравнение имеет корень x = -3/(b+5), причём имеет корень, когда -3/(b+5)≥0, то есть, при b<-5, а при b > -5 корень не имеет.
при b ≥ 5 уравнение корней не имеетпри -5 ≤ b < 5 уравнение имеет один кореньпри b < -5 уравнение имеет два различных корня.если решить как ваше уравнение то корень будет иррациональным так как по схеме горнера уже после 3 проверки идут корни очень плохие!
(5x)^(2x+1) = 5^(2x+1)*x^(2x+1) = 5*5^(2x)*x^(2x+1)
5*5^(2x)*x^(2x+1) + 5^(2x) = 5^(2x)*(5*x^(2x+1) + 1) = 750 = 6*5^3
Варианты:
{ 5^(2x) = 5^3, x = 3/2
{ 5*x^(2x+1) + 1 = 6, 5*x^(2x+1) = 5, x^(2x+1) = 1, (3/2)^4 = 1 - не подходит
{ 5^(2x) = 5^2, x = 1
{ 5*x^(2x+1) + 1 = 30, 5*x^(2x+1) = 29 - не подходит
{ 5^(2x) = 5, x = 1/2
{ 5*x^(2x+1) + 1 = 150, 5*x^(2x+1) = 149 - не подходит
{ 5^(2x) = 1, x = 0
{ 5*x^(2x+1) + 1 = 750, 5*x^(2x+1) = 749 - не подходит
может ошибка у вас там так как
(5)^(2x+1) +5^2x = 750
5^2x*5+5^2x=750
5^2x=t
6t=750
t=125
2x=3
x=3/2
теперь ставим
3/2^2+3/2 = 15/4
Область определения (или значения) функции - это ряд тех аргументов, при которых функция имеет смысл. Существует три случая в области определения определения функции:
1) если в правой части функции есть дробь, то знаменатель дроби не должен равняться нулю, в противном случае функция не имеет смысла : у=1/х - x \neq 0(в данном случае область определения функции от - бесконечности до +бесконечности, кроме нуля); y= 5/(x^2-1) - x^2-1 /neq 0 x^2 /neq 1 x /neq 1(область определения данной функции включает значения от - бесконечности до + бесконечности, исключая 1).
2) если функция имеет корень чётной степени, то значение под корнем не должно быть меньше нуля: y=корень из(х) - х>0, значит область определения функции составляет (0;+\infty).
3) если функция имеет и корень и дробь, тогда выражение под корнем не должно быть отрицательным, а выражение в знаменателе не должно равняться нулю: y=корень из(1/х+1), занчит, 1/х+1 > 0 х>-1 и х+1 /neq 0 x /neq -1(область определения этой функции содержит значения от -1 до плюс бесконечности).
У фукции y=x^2-4x+6 нет ни корней, ни дробей, поэтому область определения этой функции включает все значения числовой прямой.;)
(см. объяснение)
Объяснение:
Самый верный решить любой параметр - это постараться построить его в координатах (b; x).
Попробуем применить этот прием здесь.
Сначала заметим, что при равенство неверно при любом значении параметра. Тогда на протяжении решения при необходимости будем спокойно делить на
равенство неверно при любом значении параметра. Тогда на протяжении решения при необходимости будем спокойно делить на  .
.
Раскроем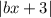 :
:
Видим гиперболу в координатах (b; x).
Построим ее и просчитаем знаки в областях, которые она образует, подставляя координаты соответствующих точек в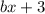 .
.
Тогда при :
:
Строим фрагмент этого графика в определенных выше областях.
При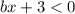 :
:
Тоже строим фрагмент этого графика в определенных выше областях.
Получим график уравнения:
(см. прикрепленный файл)
Итого:
ПриЗадание выполнено!