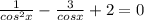
![lim_{x\to \infty }\frac{x+1}{x-2}=lim_{x\to \infty }\frac{\frac{x}{x}+\frac{1}{x}}{\frac{x}{x}-\frac{2}{x}}=lim\frac{1+\frac{1}{x}}{1-\frac{2}{x}}=[\frac{1+0}{1-0}]=\frac{1}{1}=1](/tpl/images/0237/6916/b2fde.png)
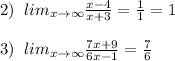
![lim_{x\to \infty }\frac{x+3}{5x^2+2x-5}=0,tak\; \; kak\\\\lim_{x\to \infty }\frac{\frac{x}{x^2}+\frac{3}{x^2}}{\frac{5x^2}{x^2}+\frac{2x}{x^2}-\frac{5}{x^2}}=lim\frac{\frac{1}{x}+\frac{3}{x^2}}{5+\frac{2}{x}-\frac{5}{x^2}}=[\frac{0+0}{5+0-0}]=\frac{0}{5}=0](/tpl/images/0237/6916/32e6e.png)
ОКАНЧИВАЕТСЯ НА 4.
1)ЧИСЛО 2 В СТЕПЕНИ 99 ОКАНЧИВАЕТСЯ НА ЦИФРУ 8.
если составить небольшую табличку,
2 в степени 1 оканчивается на 2
2 2 4
2 3 8
2 4 6
если продолжать дальше,то последовательность чисел будет постоянно повторяться,то есть любая степень числа 2 может оканчиваться на 2,4,8 или на 6 (ну,еще есть 2 в степени ноль,но это только единичный случай)
с этой таблички вычисляем,что 2 в степени 99 оканчивается на цифру 8.
2) теперь смотрим таблицу умножения на 7.
число,оканчивающееся на цифру 8 - только 28 (4*7=28),соответственно,при делении на 7 числа,оканчивающегося на цифру 8 может получиться только число,оканчивающееся на цифру 4.
1 / cos(x)^2 - 3 / cos(x) + 2 = 0
так как cos(x) != 0, так как иначе было бы деление на 0, а этого делать нельзя, то умножим обе части уравнения на cos(x)^2. Получаем:
1 - 3cos(x) + 2cos(x)^2 = 0
переставим слагаемые в удобном для нас виде:
2cos(x)^2 - 3cos(x) + 1 = 0
Заметим, что это квадратное уравнение относительно cos(x). Решим его:
D = (-3)^2 - 4 * 2 * 1 = 9 - 8 = 1
cos_1(x) = (-(-3) + sqrt(1)) / (2 * 2) = (3 + 1) / 4 = 4 / 4 = 1
cos_2(x) = (-(-3) - sqrt(1)) / (2 * 2) = (3 - 1) / 4 = 2 / 4 = 1 / 2
cos(x) = 1 при x = 2пn, где n - целое
cos(x) = 1 / 2 при x = п / 4 + 2пk, где k - целое
Наш ответ это совокупность решений для этих двух корней.
ответ: x = 2пn, где n - целое U x = п / 4 + 2пk, где k - целое