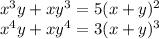
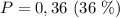
Объяснение:
Решим задачу через геометрическое определение вероятности.
Обозначим за х и у время прихода пассажиров:
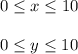
В прямоугольной системе координат этому условию удовлетворяют точки, лежащие внутри квадрата. Пассажиры встретятся, если между моментами их прихода пройдет не более 2 минут, то есть:
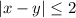
Что равносильно следующей системе:
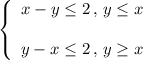
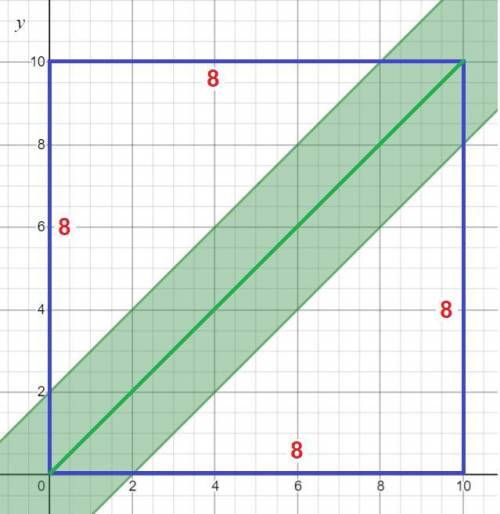
На графике такая область выглядит следующим образом (см. рисунок).
Тогда вероятность встречи равна отношению площади закрашенной области к площади всего квадрата.
Площадь закрашенной области равна разности площади квадрата и двух прямоугольных треугольников с катетами 10-2=8 .
Тогда:
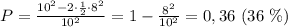
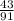
Объяснение:
Всего шаров 6+8 = 14
Вероятность того, что первый шар будет черным:
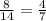
После того, как вынули черный шар, в ящике осталось 13 шаров, из которых 7 черных.Теперь вероятность того, что вытянутый шар будет черным:
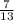
Вероятность того, что оба вынутых шара будут черными:
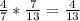
Теперь вычислим вероятность вынуть два белых шара.
Вероятность вынуть белый шар:
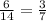
Вероятность вынуть второй белый шар:
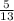
Вероятность того, что оба вынутых шара будут белыми:
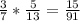
Теперь наконец-то вычислим вероятность того, что вынут два шара одного цвета (т.е. вынут два черных шара или два белых шара), используя правило сложения:
 .
.
Рассмотрим случай, когда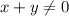
Умножим первое уравнение на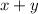 , если в результате решения системы получим решение, в котором
, если в результате решения системы получим решение, в котором 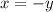 , то исключаем его.
, то исключаем его.
Используя второе уравнение системы, получаем:
Поскольку: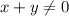
Преобразуем первое уравнение системы:
Откуда получаем:
Осталось рассмотреть случай:
Подставляя в первое уравнение системы получаем:
Нетрудно убедится, что они удовлетворяют и второму уравнению системы: