11 тетрадей по 2,2 и 5 тетрадей по 4,5.
Объяснение:
Ее и усно можно решить, если заметить, что обязательно будет нечетное количество одних тетрадей и нечетное других. Потом 46,7-2,2-4,5=40 грн.
А 40 грн. получится только если купить 10 тетрадей по 2,2 и 4 тетради по 4,5. Значит всего 11 тетрадей по 2,2 и 5 тетрадей по 4,5.
А уравнение 2,2x+4,5(16-x)=46,7
2,2x+72-4,5x=46,7
-2,3x=46,7-72
x=25,3/2,3
x=11
Дано:
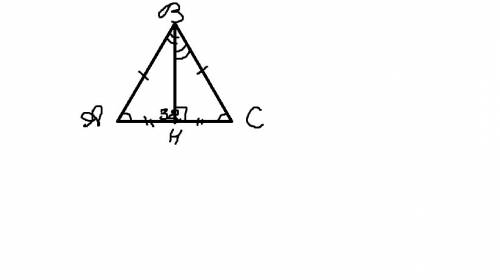
АBC - равнобедренный треугольник.
АС=32
АВ=ВС(боковые стороны)
tg A = 5/4
s-?
Проведем высоту BH. Т.к. треугольник равнобедренный, то она также биссектриса и медиана. Получим 2 прямоугольных треугольника ABH и HBC.
tg A=BH/AH(отношение противолежащего катета к прилежащему)
Т.к. BH медиана, АН=32/2=16
По условию tg A=5/4, значит BH и АН можно представить как 5х и 4х соответственно.
АН=16=4х, х=4
ВН=5х=5*4=20
Площадь треугольника равна половине произведения основания на высоту:
Основание АС=32, Высота - 20.
Следовательно s=(32*20)/2=320
ответ:320
Пусть х - тетради по 2,2 грн, тогда (16 - х) - тетради по 4,5 грн. За всю покупку заплатили 46,7 грн. Уравнение:
2,2 · х + (16 - х) · 4,5 = 46,7
2,2х + 72 - 4,5х = 46,7
72 - 46,7 = 4,5х - 2,2х
25,3 = 2,3х
х = 25,3 : 2,3
х = 11 (шт.) - тетради по 2,2 грн.
16 - 11 = 5 (шт.) - тетради по 4,5 грн.
ответ: 11 шт по 2,2 грн. и 5 шт. по 4,5 грн.