1) -35/3; -140/3; -560/3; -2240/3
2) 7; -28; 112; -448
Объяснение:
b₁, b₂, b₃, b₄-числа образующие геометрическую прогрессию⇒b₂=qb₁, b₃=q²b₁, b₄=q³b₁
b₁-b₂=35
b₃-b₄=560
b₁-qb₁=35
q²b₁-q³b₁=560
b₁(1-q)=35
q²b₁(1-q)=560
q²=560/35=16⇒q=±4
1) q=4
b₁=35/(1-q)=-35/3
b₂=qb₁=4·(-35/3)=-140/3
b₃=qb₂=4·(-140/3)=-560/3
b₄=qb₃=4·(-560/3)=-2240/3
2) q=-4
b₁=35/(1-q)=7
b₂=qb₁=-4·7=-28
b₃=qb₂=-4·(-28)=112
b₄=qb₃=-4·112=-448
Скорее всего здесь речь идет об убывающей геометрической прогрессии...
для убывающей геометрической прогрессии Sn -> b1 / (1-q)
b1 / (1-q) = 3/4 ___ 4b1 = 3(1-q)
и сумма кубов тоже будет убывающей... => Sn3 -> (b1)^3 / (1-q^3)
(b1)^3 / (1-q^3) = 27/208
27(1-q)^3 / (64(1-q^3)) = 27/208
(1-q)^3 / ((1-q)(1+q+q^2)) = 4/13
(1-q)^2 / (1+q+q^2) = 4/13
13(1-2q+q^2) = 4(1+q+q^2)
13-26q+13q^2 - 4-4q-4q^2 = 0
3q^2 - 10q + 3 = 0
D = 100 - 4*9 = 64
q1 = (10 + 8)/6 = 3 ___ q2 = (10 - 8)/6 = 1/3
b1 = 1/2
Сумма квадратов членов прогрессии = (b1)^2 / (1-q^2) = 1/4 : 8/9 = 1/4 * 9/8 = 9/32
Два варианта:
7, -28, 112, -448
Объяснение:
q=±4,
b1=7, q=-4
b1=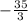 q=4
q=4