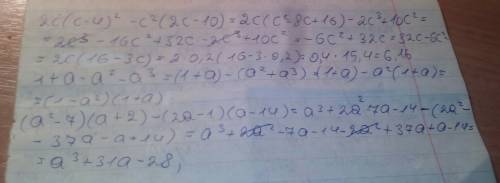
Объяснение:
Уравнение касательной к графику функции f(x) в точке х = х0 имеет следующий вид:
у = f'(x0) * (х - х0) + f(x0).
Найдем производную функции f(x) = x² + 2:
f'(x) = (x² + 2)' = 2x.
Найдем значение производной функции f(x) = x² + 2 в точке х0 = 1:
f'(1) = 2 * 1 = 2.
Найдем значение функции f(x) = x² + 2 в точке х0 = 1:
f(1) = 1² + 2 = 1 + 2 = 3.
Составляем уравнение касательной к графику функции f(x) = x² + 2 в точке х0 = 1:
у = 2 * (х - 1) + 3.
Упрощая данное уравнение, получаем:
у = 2х - 2 + 3;
у = 2х + 1.
ответ: уравнение касательной к графику функции f(x) = x² + 2 в точке х0 = 1: у = 2х + 1.
Объяснение:
y= -7x+6 (4; 8)
у нас график прямая линия. строим его по двум точкам (можем даже брать точки, не входящие в интервал)
x = 0 y(5) = 6
х = 1 у(1) = -1
а потом ограничиваем прямую по оси ох от 4 до 8, т.е. все где х < 4
и х >8 убираем