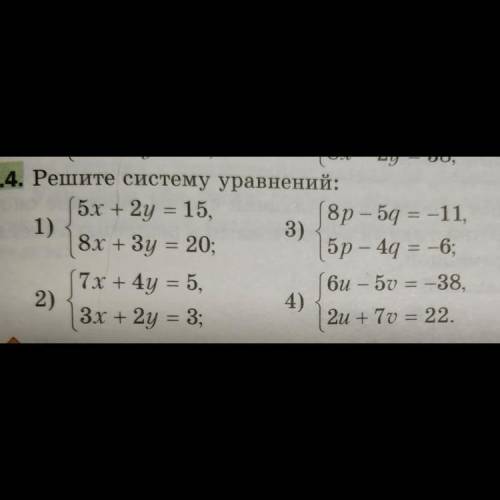
1) домножим левую и правую части на x. чтобы избавиться от дроби
3x^2 + 3 = 6x
3x^2 - 6x + 3 = 0
D = b^2 - 4ac = (-6)^2 - 4 *3 * 3 = 36 -36 = 0. [1 корень]
x= -b /2a = 6 / 6 =1
ответ: 1
2) приводим дроби к общему знаменателю
к первой дроби доп.множитель Х, ко второй (x^2 +2)
3x - (x^2 +2) -x^2 + 3x - 2
-->
x (x^2 + 2) x (x^2 + 2)
система:
{-x^2 + 3x - 2 = 0
{x (x^2 + 2) 0
-x^2 + 3x - 2 = 0
D = b^2 - 4ac = 9 - 8 = 1 2 корня
x1,2 = -b ± √D / 2a
x1 = -3 + 1 /-2 = -2/-2 = 1
x2 = -3 -1 / -2 = -4/-2 = 2
ответ: 1;2
фото прикреплю, так легче
Для определения значения тригонометрической функции, найдите его на пересечении строки с указанием тригонометрической функции. Например, синус 30 градусов - ищем колонку с заголовком sin (синус) и находим пересечение этой колонки таблицы со строкой "30 градусов", на их пересечении считываем результат - одна вторая. Аналогично находим косинус 60 градусов, синус 60 градусов (еще раз, в пересечении колонки sin (синус) и строки 60 градусов находим значение sin 60 = √3/2 ) и т.д. Точно так же находятся значения синусов, косинусов и тангенсов других "популярных" углов.
Объяснение:
Arcsin(ctg(π/4))=arcsin(1)=π/ 2 cos(arcsin(-1/2)-arcsin(1))=cos(2π/3-π/2)= cos(4π/6-3π/6)=cos(π/6)=√3/2.
2) (-1; 3) 3) (-2; -1) 4) (-3; 4)
Объяснение:
2)
7х + 4у = 5 |·3 21x + 12y = 15 Вычитаем 1-е уравнение из 2-го
3х + 2у = 3 |·7 21x + 14y = 21 2у = 6 ⇒ у = 3
7х + 4у = 5 7x + 4y = 5 Вычитаем 2-е уравнение из 1-го
3х + 2у = 3 |·2 6x + 4y = 6 х = -1
3)
8р - 5q = -11 |·5 40p - 25q = -55 Вычитаем 2-е уравнение из 1-го
5p - 4q = -6 |·8 40p - 32q = -48 7q = -7 ⇒ q = -1
8р - 5q = -11 |·4 32p - 20q = -44 Вычитаем 2-е уравнение из 1-го
5p - 4q = -6 |·5 25p - 20q = -30 7p = -14 ⇒ p = -2
4)
6u - 5v = -38 6u - 5v = -38 Вычитаем 1-е уравнение из 2-го
2u + 7v = 22 |·3 6u + 21v = 66 26v = 104 ⇒ v = 4
6u - 5v = -38 |·7 42u - 35v = -266 Cкладываем уравнения
2u + 7v = 22 |·5 10u + 35v = 110 52u = -156 ⇒ u = -3