рівняння не має розв'язків
Объяснение:
5х²+8/х²-16 - 2х-1/х+4 + 3х-1/4-х, х≠-4, х≠4
5х²+8/х²-16 - 2х-1/х+4 + 3х-1/4-х=0
5х²+8/(х-4)(х+4)- 2х-1/х+4 +3х-1/-(х-4)=0
5х²+8/(х-4)(х+4) - 2х-1/х+4 - 3х-1/х-4=0
5х²+8-(х-4)(2х-1)-(х+4)(3х-1)/ (х-4)(х+4)=0
5х²+8-(2х²-х-8х+4)-(3х²-х+12х-4)/ (х-4)(х+4)=0
5х²+8-(2х²-9х+4)-(3х²+11х-4)/ (х-4)(х+4)=0
5х²+8-2х²+9х-4-3х²-11х+4/ (х-4)(х+4)=0
5х²+8-2х²+9х-3х²-11х/ (х-4)(х+4)=0
0+8+9х-11х/ (х-4)(х+4)=0
0+8-2х/ (х-4)(х+4)=0
8-2х/ (х-4)(х+4)=0
-2х+8/ (х-4)(х+4)=0
-2(х-4)/ (х-4)(х+4)=0
-2/ х+4=0
- 2/ х+4=0
2/ х+4=0
2=0
рівняння не має розв'язків
В решении.
Объяснение:
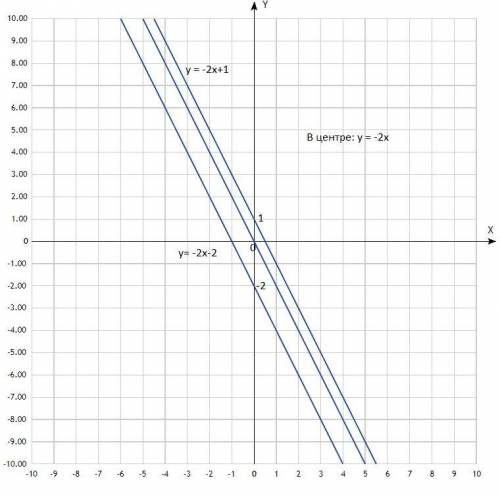
Построить на одной координатной плоскости графики функций:
у= -2х, у= -2х+1, у= -2х-2.
Построить графики. Графики линейной функции, прямые линии. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
у= -2х у= -2х+1 у= -2х-2
Таблицы:
х -1 0 1 х -1 0 1 х -1 0 1
у 2 0 -2 у 3 1 -1 у 0 -2 -4
По вычисленным точкам построить прямые.
Вывод по построению: если коэффициенты перед х равны (k₁=k₂=k₃), графики данных линейных функций параллельны.
Время против теч. - 6ч;
Собст. скорость - 10 км/ч;
Весь путь - 132 км;
Скорость течения - ? км/ч.
Установим, что a км/ч - скорость течения. Тогда по теч. мот. лодка плыла со скоростью (10 + а) км/ч, а против (10 - а) км/ч. Тогда за 7 ч мот. лодка путь в 7(10 + а) км, а за 6 ч против 6(10 - а) км. Все путешествие лодки составило 132 км, значит:
7(10 + а) + 6(10 - а) = 132;
70 + 7а + 60 - 6а = 132;
7а - 6а + 130 = 132;
а = 132 - 130;
а = 2 (км/ч) - скорость теч.
ответ: 2 км/ч.