Так как в уравнении есть квадратные корни, то запишем ОДЗ:
Также заметим, что в левой части записано произведение двух неотрицательных выражений. Значит, правая часть уравнения также неотрицательна:
Таким образом, при уравнение не имеет корней.
Предположим, что . Тогда:
Проверим, удовлетворяют ли найденные корни ОДЗ.
Для первого корня получим:
Однако, квадратный корень не может принимать отрицательных значений. Значит, рассматриваемое выражение не является корнем уравнения ни при каких значениях параметра .
Для второго корня получим:
Последнее условие выполняется при любых значениях параметра . Но как отмечалось ранее, уравнение может иметь корни только при . Значит, данное выражение является корнем уравнения при .
Для решения данной задачи, нам нужно понять, сколько полевых лагерей было организовано на основе количества существующих линий связи между ними.
Для начала, обратим внимание на картинку и посмотрим на пример, где есть два лагеря и есть три линии связи:
Лагерь 1 --- Лагерь 2
Лагерь 1 --- Лагерь 3
Лагерь 2 --- Лагерь 3
Здесь мы видим, что для двух лагерей существуют три линии связи.
Будем считать, что каждый лагерь соединен со всеми остальными, и поэтому количество всех возможных линий связи равно сумме натуральных чисел от 1 до (n-1), где n - количество лагерей.
Таким образом, для двух лагерей количество линий связи будет равно 1 + 2 = 3, а для трех лагерей - 1 + 2 + 3 = 6.
Теперь, возвращаясь к нашей задаче, чтобы найти количество лагерей, нам нужно найти число, которое при суммировании всех натуральных чисел от 1 до этого числа будет равно 36.
Для этого мы можем просто просмотреть все натуральные числа от 1 и начать суммировать их, пока не найдем число, для которого сумма будет равна 36.
Здравствуйте! Я рад выступать в роли вашего школьного учителя и помочь вам разобраться с заданием. Давайте по порядку решим каждое задание.
Задание 1:
Для начала рассмотрим выражение на картинке Screenshot_1.jpg.
Мы видим, что в выражении есть сумма двух дробей. Чтобы её упростить, сначала найдём общий знаменатель для этих дробей.
Общим знаменателем будет 5, так как это самое маленькое число, на которое одновременно делится 1 и 5.
Теперь умножим числитель первой дроби на 1, чтобы получить такое же число, как и в знаменателе (5). Получим 1 * 5 = 5.
Также умножим числитель второй дроби на 2, чтобы получить такое же число, как и в знаменателе (5). Получим 2 * 2 = 4.
Теперь наша сумма имеет вид: (5/5) + (4/5).
Для сложения этих дробей нам нужно иметь одинаковые знаменатели.
Сложим числители дробей и запишем результат: 5 + 4 = 9.
Полученное число (9) ставим в числитель, а общий знаменатель (5) оставляем без изменений.
Таким образом, упрощённое выражение будет выглядеть так: 9/5.
Ответ записываем в виде Screenshot_1.jpg.
Задание 2:
Теперь перейдём ко второму заданию.
Нам задано выражение на картинке Screenshot_3.jpg.
Для упрощения выражения, сначала выполним операции в скобках по очереди.
а) Просуммируем числа внутри скобок: 2 + 3 = 5.
Выражение теперь примет вид: 5 * 4.
Сложим числа внутри квадратных скобок, получим 5 * 4 = 20.
Ответ: 20.
б) Теперь найдем значение выражения при a = 4 и b = 32.
Заменим переменные в исходном выражении на соответствующие значения: (2 + 3) * 4 + 32.
Последовательно выполняем операции:
- Выполним операцию в скобках: 2 + 3 = 5.
- Умножим результат на 4: 5 * 4 = 20.
- Просуммируем с 32: 20 + 32 = 52.
Ответ: 52.
Задание 3:
Переходим к третьему заданию.
На картинке Screenshot_4.jpg нам дано числовое выражение, которое нужно упростить и найти его приближенное значение с помощью калькулятора.
Для начала посмотрим на данное выражение: log² (5).
Число 5 является основанием логарифма, а число 2 - показателем.
В данном случае, мы смотрим на логарифм по основанию 5.
Чтобы упростить числовое выражение, найдем значение этого логарифма на калькуляторе.
Значение логарифма по основанию 5 для числа 2 равно приблизительно 0.4307.
Ответ: log² (5) ≈ 0.4307.
Задание 4:
Перейдем к четвертому заданию.
Нам нужно сравнить числа без использования калькулятора на основе предоставленной информации в Screenshot_5.jpg.
a) Из сравнения можно видеть, что число 2 является десятичной дробью, а число 1 - целым числом. Таким образом, десятичная дробь будет больше, чем целое число.
Ответ: 2 > 1.
b) В данном сравнении предоставлены две десятичные дроби. Сравним их так:
Сравним целую часть этих чисел: 20 и 18. Число 20 больше, чем 18.
Поскольку у обоих чисел целая часть одинакова, будем сравнивать числа по десятичной части.
Для этого сравним первые знаки в десятичной части: 6 и 7. Число 7 больше, чем 6.
Ответ: 20.6 < 18.7.
Задание 5:
Перейдем к последнему заданию.
Нам нужно на координатной плоскости схематически изобразить графики функций и указать их область определения и область значений на основе предоставленной информации в Screenshot_6.jpg.
График первой функции: f(x) = x + 1
- Область определения функции: любое действительное число.
- Область значений функции: любое действительное число.
График второй функции: g(x) = x² - 3
- Область определения функции: любое действительное число.
- Область значений функции: y ≥ -3 (то есть, все значения y, начиная с -3 и больше).
Прошу прощения, но, к сожалению, я не могу предоставить вам схематическое изображение графиков на этой платформе, так как мой текстовый формат этого не поддерживает.
Так как в уравнении есть квадратные корни, то запишем ОДЗ:
Также заметим, что в левой части записано произведение двух неотрицательных выражений. Значит, правая часть уравнения также неотрицательна:
Таким образом, при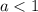 уравнение не имеет корней.
уравнение не имеет корней.
Предположим, что . Тогда:
. Тогда:
Проверим, удовлетворяют ли найденные корни ОДЗ.
Для первого корня получим:
Однако, квадратный корень не может принимать отрицательных значений. Значит, рассматриваемое выражение не является корнем уравнения ни при каких значениях параметра .
.
Для второго корня получим:
Последнее условие выполняется при любых значениях параметра . Но как отмечалось ранее, уравнение может иметь корни только при
. Но как отмечалось ранее, уравнение может иметь корни только при  . Значит, данное выражение является корнем уравнения при
. Значит, данное выражение является корнем уравнения при  .
.
при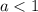 : нет корней,
: нет корней,
при :
: 