Question

дві бригади працюючи разом віконують деяку роботу за 2 дні. За скільки днів цю роботу виконала б кожна бригада окремо, якщо перщій бригаді на це потрібно на 3 дні більше, ніж другій?

Answer 1

Две бригады, работая вместе выполняют некоторую работу за 2 дня. За сколько дней эту работу выполнила бы каждая бригада в отдельности, если первой бригаде на это нужно на 3 дня больше, чем второй?

Решение.

Пусть за $x$ дней всю работу выполнила бы первая бригада, тогда

за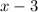  $x-3$   дней всю эту работу выполнила бы вторая бригада.

Примем весь объём работы за 1 (единицу), тогда

$\frac{1}{x}$  -  производительность первой бригады;

$\frac{1}{x-3}$   -  производительность первой бригады.

$\frac{1}{2}$  -  общая производительность двух бригад.

Уравнение:

$\frac{1}{x}+ \frac{1}{x-3} =\frac{1}{2}$        ($x3)$

$\frac{1}{x}+ \frac{1}{x-3} -\frac{1}{2} =0$

$\ \frac{2(x-3)+2x-x(x-3)}{2x(x-3)} =0$

$2(x-3)+2x-x(x-3)=0$

$2x-6+2x-x^2+3x=0$

$-x^2+7x-6=0$

$x^2-7x+6=0$

$D=49-4*1*6=25=5^2$

$x_1=\frac{7-5}{2} =1$  

           $x_1=1$  не удовлетворяет условию, т.к. $x3$

$x_2=\frac{7+5}{2} =6$  

         $x_2=6$  удовлетворяет условию.

За 6 дней всю работу выполнила бы первая бригада.

За  6-3=3  дня всю эту работу выполнила бы вторая бригада.

ответ: 6 дней; 3 дня.