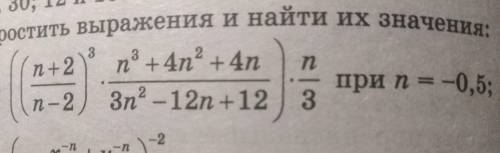
Обычно линейное уравнение определяется, как уравнение вида:
ax + b = 0 (основная формула линейного ура-я), где а и b – любые числа.
Например: 2х+7=0, в данном случае а=2, b=7.
Теперь рассмотрим пример с подробным решением:
х - 3 = 2 - 4х (переносим все неизвестные влево (значением с буквами), известные вправо (обычные цифры) , при этом меняем знаки на противоположные, получим:
х+4х=2+3 (вычисляем), получаем такое вот сокращённое ура-е:
5х=5 (чтобы найти х мы должны: правую часть разделить на цифру при переменной х):
х=5:5 , х=1
1) Сложение отрицательных чисел. Возьмем пример -3+(-3)= Оба числа отрицательны, так что получаем, по сути, -3-3= Теперь достаточно сложить модули этих чисел и вписать перед ними минус, так как он, повторюсь, отрицательны
2) Сложение отрицательных и положительных чисел. Допустим, мы имеем пример -7+5=... Чтобы его решить, необходимо вычесть из числа с большим модулем число с меньшим модулем, не учитывая при этом знаки. 7-5=2. Потом мы подпишем знак минус перед двойкой, потому что у числа с большим модулем (семерки) значение было отрицательным.
Теперь важное примечание.
+- дают минус
-- дают плюс
Так что, если нам встретиться пример вроде 5-(-3), мы преобразуем его в 5+3 и получим 8
Объяснение:
Можно попытаться сократить.
n^3 + 4n^2 + 4n = n(n^2 + 4n + 4) = n(n+2)^2
3n^2 - 12n + 12 = 3(n^2 - 4n + 4) = 3(n-2^2
Получаем:
[(n+2)^3 / (n-2)^3 * n(n+2)^2 / (3(n-2)^2)] * n/3 = n/3 * (n+2)^5 / (n-2)^5 * n/3 =
= n^2/9 * ((n+2)/(n-2))^5
Теперь подставляем n = -0,5 = -1/2
(-0,5)^2/9 * ((-0,5+2)/(-0,5-2))^5 = (1/4)/9 * (1,5/(-2,5))^5 = 1/36 * (-15/25)^5 =
= -1/36 * (3/5)^5 = -1/36 * (0,6)^5 = -1/36 * (0,6)^2*(0,6)^3 = -0,36/36 * 0,216 =
= -1/100*0,216 = -0,00216
Похоже, что длинную дробь надо было не умножать, а делить:
[(n+2)^3 / (n-2)^3] : [n(n+2)^2 / (3(n-2)^2)] * n/3 =
= (n+2)^3 / (n-2)^3 * 3(n-2)^2 / (n(n+2))^2 * n/3 =
= 3(n+2) / (n(n-2)) * n/3 = (n+2)/(n-2) = (-0,5+2)/(-0,5-2) = 1,5/(-2,5) = -0,6