157 самый большой простой делитель числа
Объяснение:
1. 3(x - 2) = x + 2
3x - 6 = x + 2
3x - x = 2 + 6
2x = 8
x = 4
2. 5 - 2(x - 1) = 4 - x
5 - 2x - 2 = 4 - x
-2x + x = 4 -5 + 2
-x = 1
x = -1
3. (7x + 1) - (9x +3) = 5
7x + 1 - 9x - 3 = 5
7x - 9x = 5 - 1 + 3
-2x = 7
x = -3,5
4. 3,4 + 2y = 7(y - 2,3)
3,4 + 2y = 7y - 16,1
2y - 7y = -16,1 - 3,4
-5y = -19,5
y = 3,9
5. 0,2(7 - 2y) = 2,3 - 0,3(y - 6)
1,4 - 0,4y = 2,3 - 0,3y + 1,8
- 0,4y + 0,3y = 2,3 + 1,8 - 1,4
-0,1y = 2,7
y = -27
6. 2/3(1/3x - 1/2) = 4x + 2 1/2
2/9x - 1/3 = 4x + 5/2
2/9x - 4x = 5/2 + 1/3
-34/9 x = 17/6
x = -3/4
Объяснение:
а) 8/17 и 11/21
1) приведём дроби к НОЗ:
21 = 3 * 7
17 = 17
НОК (17; 21) = 3 * 7 * 17 = 357
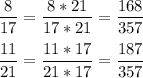
2) сравним дроби:
правило: из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше
Т.к. 187 > 168, значит:
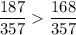 т.е.
т.е. 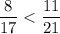
б) 0,6 и 4/7
1) т.к. дробь 4/7 не перевести в десятичную, переведём десятичную дробь 0,6 в обыкновенную:
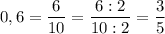
2) приведём дроби к НОЗ:
5 и 7 - простые числа
НОК (5; 7) = 5 * 7 = 35
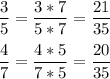
3) сравним дроби:
правило: из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше
Т.к. 21 > 20, значит:
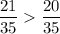 т.е.
т.е. 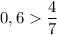
M=93*94*95*161*162
делители 93,94,95,,161,162 из них надо найти самый большой простой делитель
так как остальные делители, получаются перемножением вышеперечисленных делителей, то надо искать среди вышеперечисленных
простые числа 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163
самый большой простой делитель 157