ответ: (3;-3).
Объяснение:
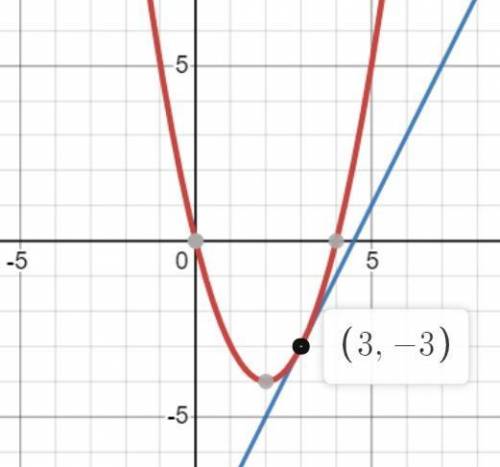
в какой точке пересекаются графики функций f(x) =x(x-4) и g(x) =2x-9?
Чтобы ответить на этот вопрос, необходимо функции приравнять и решить его: f(x)=g(x):
x(x-4)=2x-9;
x^2-4x=2x-9;
x^2-6x+9=0;
по т. Виета
x1+x2=6; x1*x2=9;
x1=3; x2=3.
строим графики
f(3)=3(3-4)=3*(-1)=-3;
g(3)=2*3-9=6-9=-3.
См. скриншот.
Объяснение:
4а) 3x³y³ + 3x²y⁴ - 6xy² = 3xy²(x²y + xy² - 2)
4б) 2a + a² - b² - 2b = a² - b² + 2a - 2b = (a - b)(a + b) + 2(a - b)
5. x - скорость велосипедиста
x + 28 - скорость мотоциклиста
x+ 0,5(x+28) = 32
x + 0,5x + 14 = 32
1,5x = 18
x = 12 км/ч - скорость велосипедиста.
х + 28 = 12 км/ч + 28 км/ч = 40 км/ч - скорость мотоциклиста.
Проверка:
Смоделируем ситуацию - велосипедист выезжает и за час проезжает 12 км. Через полчаса после его выезда, выезжает мотоциклист и со скоростью 40 км/ч преодолевает 20 км за полчаса.
12 км + 20 км = 32 км (что означает, что задачу мы решили совершенно правильно).
(3;-3).
Объяснение:
Если графики функций пересекаются, то они равны.
х(х-4) = 2х-9
х²-4х-2х+9 = 0
х²-6х+9 = 0
(х-3)² = 0
х = 3.
у = 2*3-9 = 6-9 = -3.