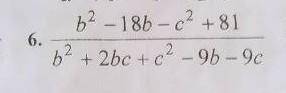
y=(x+2)^2-4 - квадратичная функция, график - парабола, ветви направлены вверх, график можно получить путём параллельного переноса графика функции y=x^2 на 2 единичных отрезка влево и на 4 единичных отрезка вниз
1) D(y)=R
2) Нули: x=0 при y=0; y=0 при x=0 и x=-4
3) y<=0 при x принадлежащем [-4;0], y>0 при x принадлежащем (-бесконечность;-4) и (0;+ бесконечность)
4) Функция убывает на промежутке x принадлежащем (-бесконечность;-2) и возрастает на промежутке x принадлежащем (-2;+ бесконечность)
5) E(y)=[-4;+бесконечность).
Подробнее - на -
Объяснение:
(a - b)² = a² - 2ab + b²
a² - b² = (a - b)(a + b)
b² - 18b - c² + 81 = (b - 9)² - c² = (b - 9 + c)(b - 9 - c)
b² + 2bc + c² - 9 - 9c = (b + c)² - 9(b + c) = (b + c)(b + c - 9)
(b - 9 + c)(b - 9 - c) / (b + c)(b + c - 9) = (b - 9 - c) / (b + c)