Объяснение:
Выражение не имеет смысла в двух случаях:
1) Когда знаменатель дроби равен нулю, или вообще если в выражении встречается деление на ноль, так как мы все помним, что "на ноль делить нельзя". К примеру: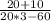 
или 
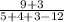
В знаменателе мы получаем нуль, и совсем не важно, какое значение получится в числителе.
2) Или в случае, когда под корнем находится отрицательное число: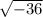 
, так как невозможно выделить корень из отрицательного числа.
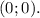
Объяснение:
Данная функция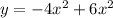 
является квадратичной функцией (многочлен второй степени) и задаёт квадратичную параболу. Как известно, у такой функции может быть лишь один экстремум, находящийся в вершине параболы.
Упростим исходную функцию: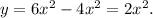 
Для нахождения 
единственного экстремума воспользуемся производной: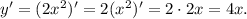 
По лемме Ферма, значение производной от экстремума нулевое. Таким образом, точки экстремума будет решением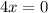 
.
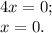
Для нахождения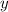 
точки экстремума вычислим значение исходной функции от найденного :
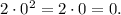
Получается, что координаты точки экстремума это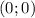 
.
x^2+7=0 не имеет смысла не имеет точек