Нельзя!
Доказательство:
Число 1 не может быть поставлено в середину ребра куба, т.к. полусумма ни одной пары оставшихся чисел не может быть равна 1. Наименьшее возможное значение такой полусуммы (2+4):2=3.
Следовательно, число 1 должно располагаться в вершине куба. Из этого вытекает, что в вершинах куба могут располагаться только нечетные числа (По условию сумма чисел, стоящих на концах ребра, должна делиться на 2 без остатка, т.е. быть четной. А сумма двух чисел, одно из которых нечетное, может быть четной только при условии, что и второе число тоже нечетное).
Из этого следует, что число 20 будет располагаться в середине какого-либо ребра куба. Очевидно, что число 20 не может быть полусуммой каких-либо двух чисел, каждое из которых меньше 20.
Вывод: расположить числа указанным в задаче невозможно.
Определить промежутки монотонности функции, не используя производную функции.
y = (x² - x - 20)² - 18
=================================
Область определения функции D (y) = R
y = (x² - x - 20)² - 18
Квадратичная функция в квадратичной функции
y = f(z); z = g(x)
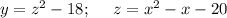
Чтобы найти промежутки монотонности квадратичной функции, нужно найти абсциссу вершины параболы.
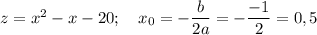 - координата вершины
- координата вершины
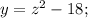 z = 0 - координата вершины параболы
z = 0 - координата вершины параболы

x₁ = -4; x₂ = 5 - координаты вершин параболы
Таким образом, есть три точки, которые определяют промежутки монотонности функции y = (x² - x - 20)² - 18.
x₁ = -4; x₀ = 0,5; x₂ = 5
x ∈ (-∞; -4] - функция убывает : y(-5) > y(-4)
x ∈ [-4; 0,5] - функция возрастает : y(-4) < y(0)
x ∈ [0,5; 5] - функция убывает : y(1) > y(2)
x ∈ [5; +∞) - функция возрастает : y(5) < y(6)
ответ:правильно?