Відповідь:
x₁ = 0,8
x₂= 1,55
Пояснення:
0,64-x²=(3x-7)(x-0,8)
0,64-x² = 3х²-2,4х-7х+5,6
0,64-x² - 3х²+2,4х+7х- 5,6 = 0
-4х²+9,4х-4,96 = 0 | *(-1)
4x²-9,4x+4,96=0
D=b²-4ac=9,4²-4*4*4,96 = 88,36-79,36 = 9
x₁= 9,4 - 3/8 = 0,8
x₂=9,4 + 3/8= 1,55
ответ: 24 см и 12 см.
Объяснение:
Пусть l - длина отрезка, соединяющего середины диагоналей трапеции. Этот отрезок лежит на средней линии трапеции и равен полуразности её оснований. Пусть a и b - основания трапеции, причём a>b, а c - длина средней линии трапеции. Так как по условию диагонали трапеции делят её среднюю линию на 3 равных части, то l=c/3. Отсюда c=3*l=3*6=18 см и, так как c=(a+b)/2, то мы получаем систему уравнений:
(a-b)/2=6
(a+b)/2=18
или:
a-b=12
a+b=36
Решая её, находим a=24 см и b=12 см.
1) Пусть x рублей - начальная цена книги, тогда на 0,1x рублей подешевела книга. Известно, что теперь она стоит 45,9 рублей.
Составляем уравнение:
x-0,1x=45,9
0,9x=45,9
x=51
ответ: 51 рубль.
2) Пусть x км/ч - собственная скорость катера, тогда (x+5) км/ч - скорость катера по течению, (х-5) км/ч - скорость катера против течения. Известно, что расстояние между пристанями катер проходит по течению реки за 2 часа, против течения - за 3 часа. Расстояние между пристанями равно 2(х+5) км или 3(х-5) км.
Составляем уравнение:
2(х+5)=3(х-5)
2х+10=3х-15
2х-3х=-15-10
-х=-25
х=25
ответ: 25 км/ч.
3) 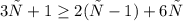
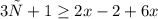
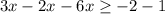
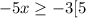
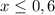
(-![(-\infty; 0,6]](/tpl/images/0028/3562/4534f.png)
4) 
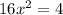
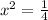
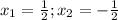
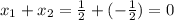
x1 = 0,8
x2= 1,55
Объяснение:
0,64-x^2=(3x-7)(x-0,8)
0,64-x^2=3х^2-2,4x-7x+5,6
0,64-x^2-3х^2+2,4x+7x-5,6=0
-4x^2+9,4x-4,96=0 | *(-1)
4x^2-9,4x+4,96=0
D=b^2-4ac=9,4^2-4*4*4,96 = 88,36 -79,36 =9
x1= (9,4 - 3)/8 = 0,8
x2=(9,4 + 3)/8= 1,55