 ,
, , a
, a 
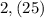
 целая часть. У нас она равна 2
целая часть. У нас она равна 2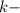 - количество цифр в периоде. У нас их 2
- количество цифр в периоде. У нас их 2 количество цифр до периода. У нас их 0
количество цифр до периода. У нас их 0 все цифры, включая период, в виде натурального числа. У нас это 25
все цифры, включая период, в виде натурального числа. У нас это 25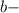 все цифры без периода в виде натурального числа. Их нет.
все цифры без периода в виде натурального числа. Их нет.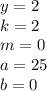
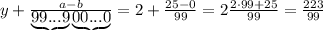
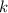 подставляется количество 9, а под
подставляется количество 9, а под  -количество нулей. У нас
-количество нулей. У нас 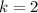 , значит пишем две цифры 9, а
, значит пишем две цифры 9, а  , значит, нулей не пишем вообще. Между
, значит, нулей не пишем вообще. Между 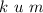 не стоит знак умножения
не стоит знак умножения
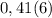

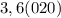

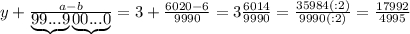
11 + 5х = 55 +3х
Всё с иксом переносим в лево, а без икса в право, при этом меняя знак на противоположный ( то есть если стоит -5, то переносим +5 и тд., если знака нет то это получается то же самое что и знак +следовательно переносим с минусом)
5х - 3х = 55 - 11
Дальше считаем
2х = 44
И находим икс
Х = 44 : 2
ответ х = 22
Так же и все остальные.
- 8х - 17 = 3х- 105
Переносим с противоположным знаком
-8 х - 3х = - 105 + 17
Считаем
11 х = - 88
Находим х
Х = - 88: 11
Х = 8
Дальше сам( а)