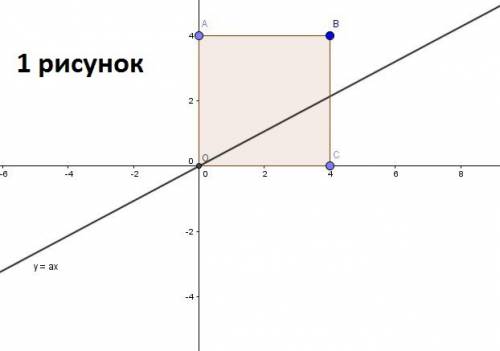
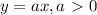 на одной координатной плоскости (смотрите первый рисунок). Отметим, что площадь фигуры, содержащей точку
на одной координатной плоскости (смотрите первый рисунок). Отметим, что площадь фигуры, содержащей точку 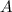 , — это площадь фигуры под точкой
, — это площадь фигуры под точкой 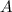 до нашей прямой. В свою очередь площадь фигуры, содержащей точку
до нашей прямой. В свою очередь площадь фигуры, содержащей точку 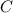 , — это площадь фигуры над точкой
, — это площадь фигуры над точкой 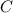 и до нашей прямой. Перейдем к решению задачи.
и до нашей прямой. Перейдем к решению задачи.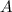 , от величины
, от величины  .
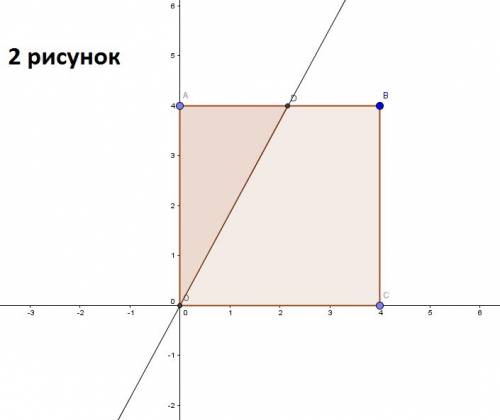
.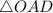 (смотрите рисунок 2). Очевидно, что размеры сторон треугольника меняются вместе с величиной
(смотрите рисунок 2). Очевидно, что размеры сторон треугольника меняются вместе с величиной  , а значит от величины
, а значит от величины  зависит и площадь треугольника. Как же найти эту площадь? Из рисунка 2 видно, что при любом значении
зависит и площадь треугольника. Как же найти эту площадь? Из рисунка 2 видно, что при любом значении 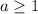 (при
(при 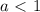 эта фигура уже не треугольник, а трапеция) треугольник остается прямоугольным, поскольку
эта фигура уже не треугольник, а трапеция) треугольник остается прямоугольным, поскольку 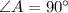 , отсюда следует, что площадь треугольника можно найти как полупроизведение катетов:
, отсюда следует, что площадь треугольника можно найти как полупроизведение катетов: 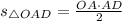 . Необходимо выразить эту площадь через величину
. Необходимо выразить эту площадь через величину  , то есть узнать, как катеты
, то есть узнать, как катеты 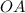 и
и 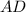 зависят от
зависят от  . Поразмышляем над этим:
. Поразмышляем над этим: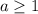 катет
катет 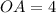 (из условия точка
(из условия точка 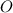 имеет координату
имеет координату 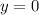 , а точка
, а точка 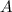 координату
координату 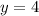 , отсюда
, отсюда 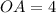 ).
). 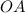 никак не зависит от величины
никак не зависит от величины  . Вы можете в этом убедиться, «покрутив» прямую, заданную функцией
. Вы можете в этом убедиться, «покрутив» прямую, заданную функцией 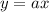 , но не забывайте, что
, но не забывайте, что 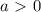 , а также то, что если мы рассматриваем случай с треугольником, то
, а также то, что если мы рассматриваем случай с треугольником, то 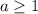 .
.  зависит катет
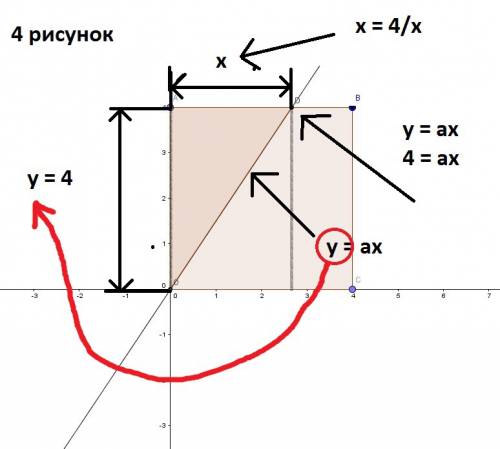
зависит катет 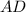 . Это не очень просто, но я постараюсь показать эту зависимость. Посмотрите на рисунок 4. Нас интересует сторона квадрата
. Это не очень просто, но я постараюсь показать эту зависимость. Посмотрите на рисунок 4. Нас интересует сторона квадрата 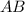 . Координата
. Координата 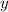 этой прямой
этой прямой 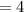 . С другой стороны, эту прямую пересекает другая прямая, заданная функцией
. С другой стороны, эту прямую пересекает другая прямая, заданная функцией 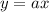 . Раз эти прямые пересекаются, значит их координаты
. Раз эти прямые пересекаются, значит их координаты 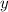 равны. Я пометил где
равны. Я пометил где  , а где
, а где 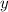 на рисунке. Так совпало, что координата
на рисунке. Так совпало, что координата  и есть искомый нами катет. Прямая задается функцией
и есть искомый нами катет. Прямая задается функцией 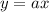 . Нас интересует тот самый
. Нас интересует тот самый  , что является катетом треугольника. То есть тот
, что является катетом треугольника. То есть тот  , который получается при
, который получается при 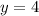 . Запишем это:
. Запишем это: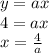
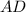 от величины
от величины  .
. 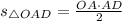
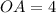 ,
, 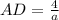 . Найдем теперь зависимость площади треугольника от
. Найдем теперь зависимость площади треугольника от  :
: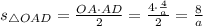
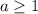 . А что будет в случае, если
. А что будет в случае, если 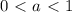 ? Подумаем.
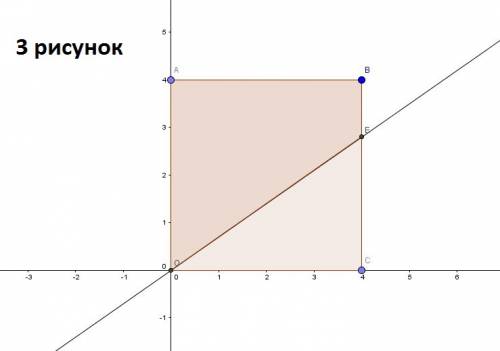
? Подумаем. 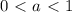 точкой
точкой 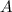 ограничена трапеция
ограничена трапеция 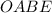 (смотрите рисунок 3). Как найти площадь трапеции? Площадь трапеции — произведение полусуммы оснований на высоту. В нашем случае имеем:
(смотрите рисунок 3). Как найти площадь трапеции? Площадь трапеции — произведение полусуммы оснований на высоту. В нашем случае имеем: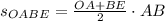
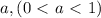 . Основание
. Основание 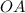 и высота
и высота 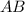 от
от  не зависят. Зависит только меньшее основание
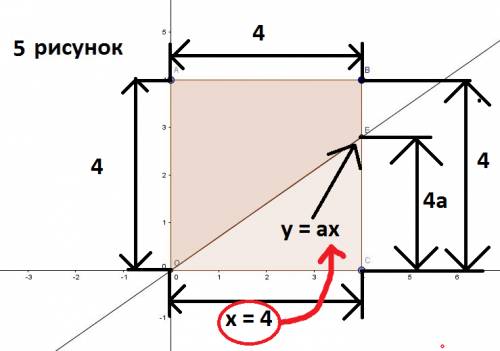
не зависят. Зависит только меньшее основание 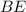 . Найдем эту зависимость (она куда проще, чем в случае с треугольником). Смотрите рисунок 5. Как видно из рисунка,
. Найдем эту зависимость (она куда проще, чем в случае с треугольником). Смотрите рисунок 5. Как видно из рисунка, 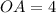 ,
, 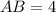 . Подумаем, какова зависимость малого основания трапеции
. Подумаем, какова зависимость малого основания трапеции 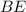 от величины
от величины  . Видим, что
. Видим, что 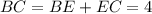
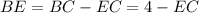
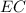 . Тут начинается та же история с пересечением двух прямых. Причем
. Тут начинается та же история с пересечением двух прямых. Причем 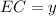 , а на этот раз
, а на этот раз 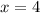 . Получаем:
. Получаем: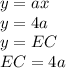
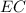
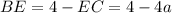 .
.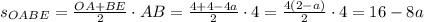
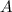 , зависит от величины
, зависит от величины  , причем по-разному (два случая). Запишем это в виде системы:
, причем по-разному (два случая). Запишем это в виде системы: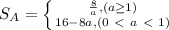
Вторая сторона равна 209 сантиметров и 40 миллиметров, иначе 209 см + 4 см = 213 сантиметров.
P = (200,5 см + 213 см) × 2 = 413,5 см × 2 = 827 сантиметров или 0,827 метра.
S = 200,5 см × 213 см = 42706,5 см² или 4,27065 м².
Странную формулировку задания ты подобрал. То ли с одним прямоугольником работать надо, то ли с двумя... Вообщем, вот решение для работы с двумя прямоугольниками.
1 прямоугольник.
P = (196 см + 45 мм) × 2 = (196 см + 4,5 см) × 2 = 200,5 см × 2 = 401 см – периметр прямоугольника со сторонами 196 сантиметров и 45 миллиметров.
S = 196 см × 45 мм = 196 см × 4,5 см = 882 см² или 0,0882 м² – площадь прямоугольника со сторонами 196 сантиметров и 45 миллиметров.
2 прямоугольник.
P = (209 см + 40 мм) × 2 = (209 см + 4 см) × 2 = 213 см × 2 = 426 см – периметр прямоугольника со сторонами 209 сантиметров и 40 миллиметров.
S = 209 см × 40 мм = 209 см × 4 см = 836 см² или 0,0836 м² – площадь прямоугольника со сторонами 209 сантиметров и 40 миллиметров.