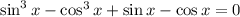
Воспользуемся формулой разности кубов:
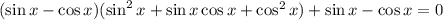
Выносим за скобки общий множитель:
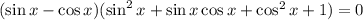
Уравнение распадается на два. Решаем первое:
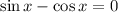
Почленно разделим на 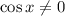 :
:
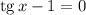
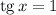
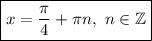
Решаем второе уравнение:
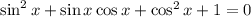
Заметим в левой части основное тригонометрическое тождество:
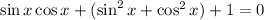
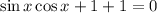
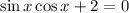
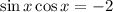
Обе части уравнения домножим на 2:
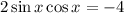
Чтобы в левой части применить формулу синуса двойного угла:
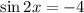
Но так как синус любого угла принимает значения только из отрезка от -1 до 1, то последнее уравнение не имеет решение.
Значит, никаких других корней, кроме найденных ранее, исходное уравнение не имеет.
ответ: 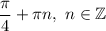
ответ: k=-1,5
Объяснение:
У тебя есть уравнение y=kx+5 и точка D(6;-19).
У точки есть координаты. Они находятся в скобках. 1ое число в скобках - координата по оси X, а 2ое число - координата по оси Y ( D(X;Y) ). В уравнении графика функции тоже есть X и Y. Я имею ввиду то, что находится в скобках надо поставить в уравнение графика функции. После подстановки у нас получается обычное уравнение (в данном случае линейное):
-19=16k+5
1) 16k=-19-5
2) 16k=-24 | /16
3) k=-24/16 (-24/16 надо сократить на 8)
4) k=-3/2
5) k=-1,5
ответ: k=-1,5