1) - "Инструкция по построению графика своими руками";
2) - Сам график;
3). - Асимптоты.
_____________________________________
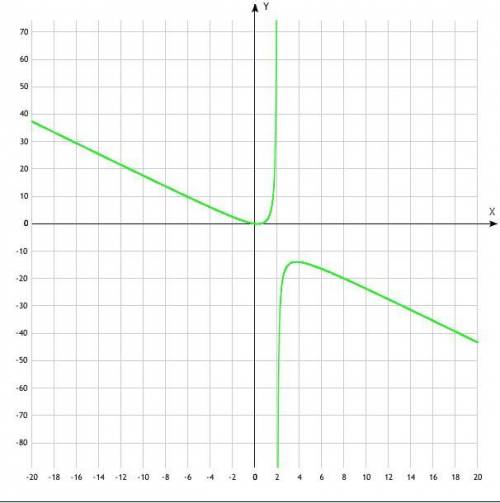
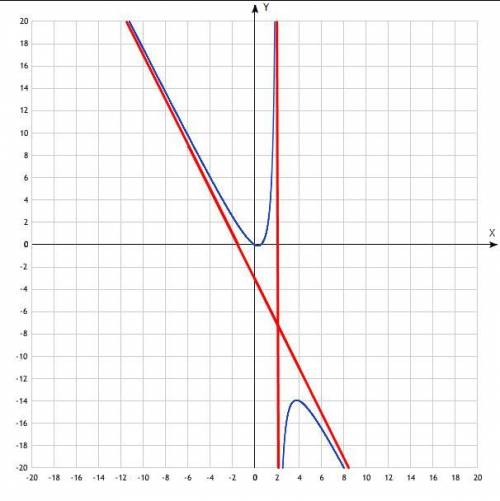
Асимптоты здесь - это вертикальная прямая, параллельная оси ординат и проходящая через точку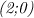 
(задается уравнением 
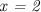) и наклонная, которая, как показывают вычисления, является графиком линейной функции 
.
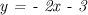Пересечения с осями координат происходят в точках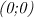 
и 
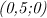. Чтобы их найти, достаточно в уравнение, задающее функцию, поочередно подставить 
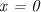и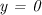 
.
А таблица точек - в прикрепленном файле.
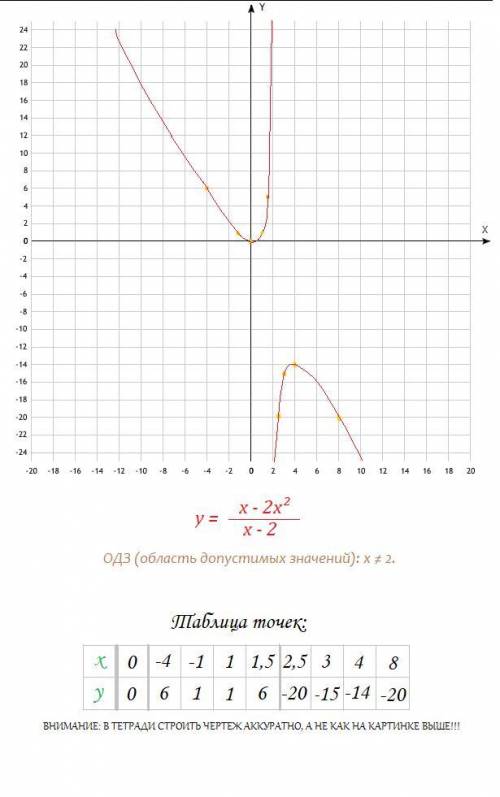
Смотри решение.
Объяснение:
решения (через дискриминант):
Порядок решения:
а. Записываем уравнение в исходном виде;
б. Находим дискриминант (дискриминант должен получиться больше 0 (2 корня уравнения), или равным 0 (1 корень уравнения), если дискриминант меньше 0, то уравнение не имеет корней, и дальше его нет смысла решать);
в. Находим корни уравнения, при условии того, что написано в предыдущем пункте.
решения (через теорему Виетта):
Сумма 2 корней уравнения равняется коэффициенту b, взятому с противоположным знаком.
Произведение 2 корней уравнения равняется свободному коэффициенту в данном уравнении.
Общая формула квадратного уравнения: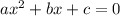
(для справок).
Теперь переходим к решению данного квадратного уравнения: