Для выполнения упрощения выражения 4x^4 * (-2x^2)^3 мы начнем с того, что одночлен возведем в третью степень и получаем выражение:
4x^4 * (-2 * x^2)^3 = 4x^4 * (-2)^3 * (x^2)^3.
Применим правило возведения степени в степень:
(a^n)^m = a^(n * m).
Применим правило и получаем:
4x^4 * (-2)^3 * (x^2)^3 = 4x^4 * (-8) * x^5.
Теперь выполняем умножения переменных и числовой части и получаем выражение:
4x^4 * (-8) * x^5 = 4 * (-8) * x^4 * x^5;
a^n * a^m = a^(n + m).
4 * (-8) * x^4 * x^5 = -32x^9.
(2;3)U(3;+ бесконечность)
Объяснение:
Рассмотрим первый знаменатель кореньх-2 должен быть больше нуля, тк знаменатель не может равняться нулю, а тк он ещё и под корнем, то меньше нуля он быть тоже не может из этого следует, что мы будем решать неравенство :
Корень х-2>0
Возводим обе части в квадрат
Х-2=0
Х=2
На координатной прямой отмечаем точку 2 и берём все значения больше 2, те (2;+бесконечность)
Теперь рассмотрим второй знаменатель
Х^2-3х≠0
Х(х-3)≠0
Х≠0 или х-3≠0
Х≠3
Теперь анализируем, то, что получили
Тк в первом знаменателе мы можем брать значения (2;+бесконечность), а во втором х≠0;3, то образуется новый промежуток (2;3)U(3;+бесконечность).
1) 7x + 4y =6; 7x + 4y-6 = 6-6; 7x + 4y - 6 =0 2) 7x + 4y =6; 4y =6-7x; y=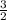 
- 
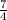x; y= -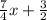
Объяснение: до першого розв'язку: переносимо число в ліву частину шляхом додавання протилежного числа до обох частин і потім сума двох протилежних чисел дорівнює 0. До другого розв'язку: переносемо змінну з протилежним знаком у праву частину потім розділяємо обидві частини рівняння на 4 і використовуємо комутативну властивість щоб змінити порядок доданків
Объяснение:
(х^2)^4×(х^4)^3=х^8*х^12=х^20