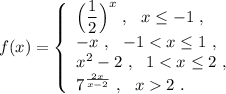
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х= -1, х=1 , х=2 .
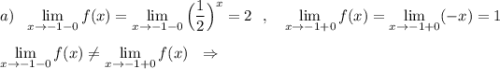
При х= -1 функция имеет разрыв 1 рода .

При х=1 функция непрерывна.
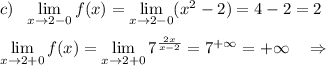
При х=5 функция имеет разрыв 2 рода .
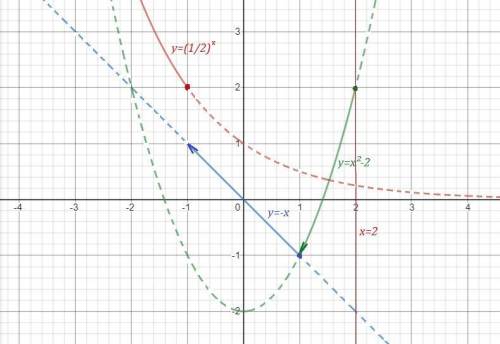
График функции нарисован сплошными линиями.
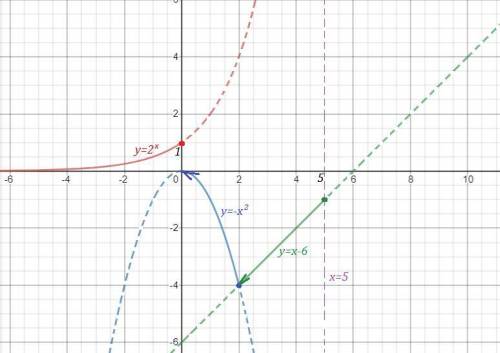
На 1 рисунке нет чертежа функции при х>2 , для которого прямая х=2 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>2 сплошной линией..
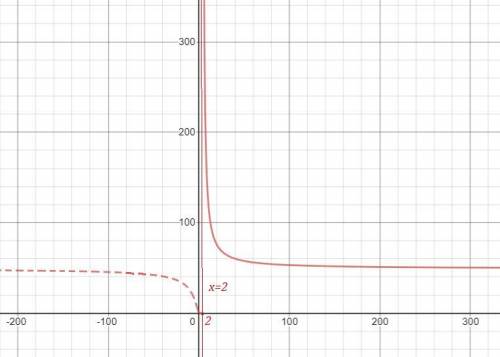
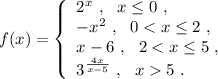
Исследуем поведение функции вблизи точек, где её аналитическое выражение меняется . Найдём левосторонние и правосторонние пределы в точках х=0, х=2 , х=5 .
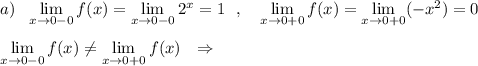
При х=0 функция имеет разрыв 1 рода .
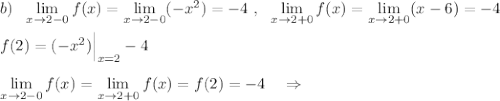
При х=2 функция непрерывна.
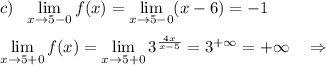
При х=5 функция имеет разрыв 2 рода .
График функции нарисован сплошной линией.
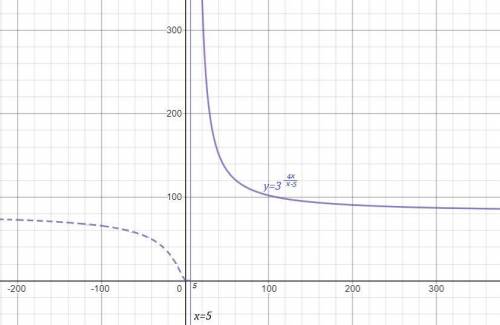
На 1 рисунке нет чертежа функции 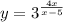 при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .
при х>5 , для которого прямая х=5 является асимптотой , так как он не умещается при данном масштабе. Этот график полностью начерчен отдельно на 2 рисунке, чтобы вы понимали, как он расположен. Но для вашей функции берётся только та часть графика, которая нарисована для х>5 .
1. x₁ = -10; x₂ = 9
2. х₁ = 8; x₂ = 6
Объяснение:
1. Решаем через дискриминант:
х²+х-90=0;
D = b²- 4ac (формула дискриминанта)
D = 1² - 4 · 1 · (-90) = 1 + 360 = 361 (Дискриминант больше нуля (361 > 0) значит у уравнения 2 корня)
√361 = 19
х₁ =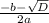
x₁ =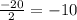
х₂ =
x₂=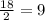
x₁ = -10; x₂ = 9
2. Решаем через дискриминант:
х²-10х-24=0
D = b²- 4ac (формула дискриминанта)
D = -10² - 4 · 1 · 24 = 100 - 96 = 4 (Дискриминант больше нуля (4 > 0) значит у уравнения 2 корня)
√4 = 2
х₁ =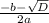
х₁ =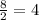
х₂ =
х₂ =
х₁ = 8; x₂ = 6
Надеюсь с: (Если что не понял пиши в комменты)