встречи будет одинаковым поэтому просто t), теперь второй велосипедист у него скорость V2, а путь S2, но сказано что первый проехал на 6 км меньше, значит второй по отношению к пути первого велосипедиста проехал на 6 км больше!, отсюда S2=S1+6. Время за которое второй доехал до места встречи t=(S1+6)/V2. Теперь смотрим что происходило после встречи: первый проехал путь второго (а это S2=S1+6) за время 2 часа 24 мин (переводим в минуты 144 мин), значит 144=(S1+6)/V1. Второй в свою очередь проехал путь первого S1 за 1 час и 40 мин (это 100 мин), значит 100=S1/V2. Вот все условия записаны. Теперь из последних двух выражений выводим: V1=(S1+6)/144 и V2=S1/100. Эти данные подставляем в первые выражения и так как t у них одинаковое, то приравниваем их:S1/V1=(S1+6)/V2, подставляем V1 и V2: 144хS1/(S1+6)=100х(S1+6)/S1, из этого получаем 144хS1*2=100х(S1+6)*2, далее 12*2хS1*2=10*2х(S1+6)*2 избавляемся от квадратов получаем 12S1=10х(S1+6) отсюда 2S1=60, S1=30 км. Вот и ответ.
| 5 - 2x| ≤ 7
5 - 2x ≤ 7; 5 - 2x ≥ 0
- ( 5 - 2x) ≤ 7; 5 - 2x < 0
x ≥ - 1; x ≤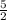
x ≤ 6; x >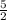
x∈ [ - 1;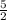 ]; x∈ (
]; x∈ (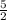 ; 6]
; 6]
x∈ [ - 1; 6]