16%
Объяснение:
допустим исходная стоимость товара х
x* 3/5 идет с наценкой 5%. то есть этот товар стал стоить на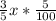 
дороже. то есть цена этого товара стала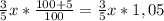 
Осталость 2/5 товара. Половина его, то есть 1/5 продавалась с наценкой 4%, то есть она стоила 1,04x*1/5
Оставшиеся 1/5 товара продавалист с неизвестной наценкой y%, она стоила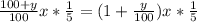 
В итоге товар стоил
1,05*x*3/5 + 1,04*x*1/5 + (1+y/100))*x*1/5= (1,05*3+1,04 +(1+y/100)x/5
с другой сторны общая наценка оказалась 7%, то есть товар стал стоить 1,07х
Получаем уравнение
(1,05*3+1,04 +(1+y/100))x/5=1,07х
Сокращаеи на х
(1,05*3+1,04 +(1+y/100))/5=1,07
1,05*3+1,04 +(1+y/100)=1,07*5
3,15+1,04 +1 +y/100=5,35
5,19 +y/100=5,35
y/100=0,16
y=16
АКСИОМА НЕПРЕРЫВНОСТИ (ПРИНЦИП ДЕДЕКИНДА)
Пусть AA, BB -- непустые подмножества RR такие, что
∀a∈A,b∈B → a≤b.∀a∈A,b∈B → a≤b.
Тогда существует c∈Rc∈R такое, что
∀a∈A,b∈B → a≤c≤b.
НЕКОТОРЫЕ СЛЕДСТВИЯ ИЗ АКСИОМ МНОЖЕСТВА ДЕЙСТВИТЕЛЬНЫХ ЧИСЕЛ
Число 0 единственно.
Для любого aa число (−a)(−a), противоположное к aa единственно.
Для любых a,b∈Ra,b∈R существует единственное xx такое, что a+x=ba+x=b (при этом x=b+(−a)x=b+(−a); это число называется разностью между bb и aa и обозначается b−ab−a).
Число 1 единственно.
1) -2; 9
2) 10;48;0.29
3) 5
4)3.28
5) 708
Объяснение:
1) 12-8х
х=-2
12-8×(-2)=12-16=-4
а=3/8
12-8×3/8=12-3=9
2) а2-3а
а=5
25-3×5=25-15=10
а=-6
36-3×(-6) =36+12=48
а=0.1
0.01-3×0.1=0.01-0.3=-0.29
3) 3m+4n
m=7
n=-4
3×7+4×(-4)=21-16=5
4) (3х-5)×у
х=0.3
у=0.8
(3×0.3-5) ×0.8=(0.9-5) ×0.8=4.1×0.8=3.28
5) (х+7298) ÷у
х=37306
у=63
(37306+7298)÷63=44604÷63=708