1) Найдем нулю нашей функции. Для чего разложим на множители формулу, которой она задана, с введения новых вс членов.
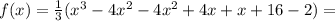
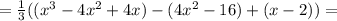
![=\frac{1}{3}[x(x-2)^{2}-4(x-2)(x+2)+(x-2)]=](/tpl/images/0065/5986/78255.png)
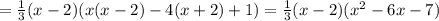
Из 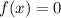 следует:
следует:
а) 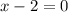 , отсюда
, отсюда 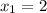 - нуль функции
- нуль функции
б) 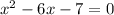 ,
, 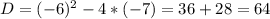 , отсюда
, отсюда
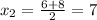 ,
, 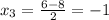 - нули функции
- нули функции
Итак, функция 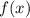 обращается в нуль в точках
обращается в нуль в точках 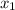 ,
, 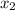 и
и 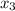
2) Найдем возможные точки экстремума нашей функции. Для чего найдем производную функции 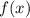 :
:
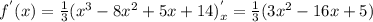 -----(1)
-----(1)
Разложим квадратный трехчлен, стоящий в правой части (1), на целые множители. Для чего найдем дискриминант этого квадратного трехчлена:
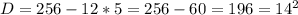 , отсюда найдем корни:
, отсюда найдем корни:
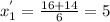
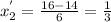 ---------(2)
---------(2)
Тогда с (2) выражение (1) примет вид метода интервалов найдем промежутки, на которых производная функции 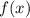 принимает положительные и отрицательные значения:
принимает положительные и отрицательные значения:
а) 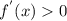 при x принадлежащем объединению промежутков
при x принадлежащем объединению промежутков
(-бесконечности; 1/3)U(5; +бесконечности )
б) 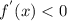 при x принадлежащем промежутку (1/3; 5)
при x принадлежащем промежутку (1/3; 5)
Известно, что промежутки, на которых производная функции положительна, являются промежутками возрастания функции!
На промежутках, где 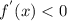 , функция убывает!
, функция убывает!
Поскольку при переходе через точку x=1/3 производная меняет знак с плюса на минус, то эта точка - точка максимума
Поскольку при переходе через точку x=5 производная меняет знак с минуса на плюс, то эта точка - точка минимума. Итак,

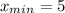
1) Найдем нулю нашей функции. Для чего разложим на множители формулу, которой она задана, с введения новых вс членов.
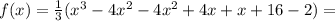
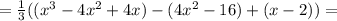
![=\frac{1}{3}[x(x-2)^{2}-4(x-2)(x+2)+(x-2)]=](/tpl/images/0065/5986/78255.png)
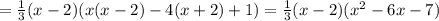
Из 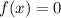 следует:
следует:
а) 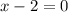 , отсюда
, отсюда 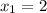 - нуль функции
- нуль функции
б) 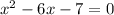 ,
, 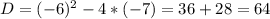 , отсюда
, отсюда
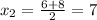 ,
, 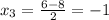 - нули функции
- нули функции
Итак, функция 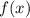 обращается в нуль в точках
обращается в нуль в точках 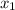 ,
, 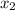 и
и 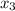
2) Найдем возможные точки экстремума нашей функции. Для чего найдем производную функции 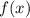 :
:
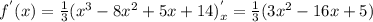 -----(1)
-----(1)
Разложим квадратный трехчлен, стоящий в правой части (1), на целые множители. Для чего найдем дискриминант этого квадратного трехчлена:
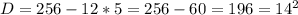 , отсюда найдем корни:
, отсюда найдем корни:
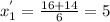
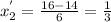 ---------(2)
---------(2)
Тогда с (2) выражение (1) примет вид метода интервалов найдем промежутки, на которых производная функции 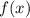 принимает положительные и отрицательные значения:
принимает положительные и отрицательные значения:
а) 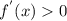 при x принадлежащем объединению промежутков
при x принадлежащем объединению промежутков
(-бесконечности; 1/3)U(5; +бесконечности )
б) 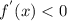 при x принадлежащем промежутку (1/3; 5)
при x принадлежащем промежутку (1/3; 5)
Известно, что промежутки, на которых производная функции положительна, являются промежутками возрастания функции!
На промежутках, где 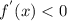 , функция убывает!
, функция убывает!
Поскольку при переходе через точку x=1/3 производная меняет знак с плюса на минус, то эта точка - точка максимума
Поскольку при переходе через точку x=5 производная меняет знак с минуса на плюс, то эта точка - точка минимума. Итак,

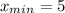
ответы выделены жирным шрифтом
Объяснение:
a)3x - 7 равно 14
3x-7 = 14
3x = 14+7
3x = 21
x=7
б) значение выражений 3x - 7 и 3 = 5x равны;
3x - 7 = 3 + 5x
3x-5x=3+7
-2x=10
x=-5
в) значение выражения x + 3 на 4 больше значения 1 - 7x.
x + 3 - (1 - 7x) = 4
x + 3 - 1 + 7x = 4
x+7x = 4-3+1
8x = 2
x = 2/8 или 1/4