x∈(-∞;-8)∪(3;+∞)
Объяснение:
(х-3)(х+8)>0
если функцию приравняем к 0, то корни уравнения будут
х-3=0
х1=3
х+8=0
х2=-8
функция пересекает ось Ох в этих точках и равна 0.
(х-3)(х+8)=х²+5х-24
а=1
b=5
c=-24
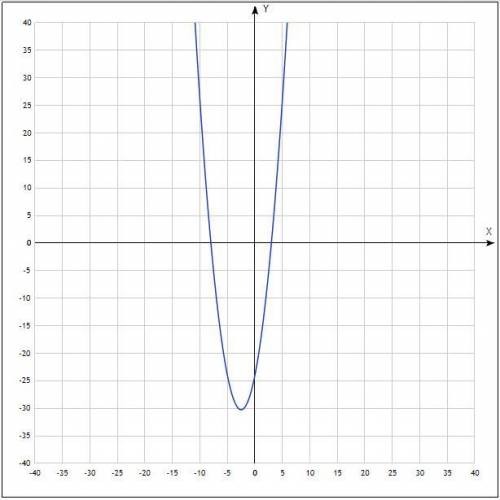
График пересекает ось Оу в точке (0;-24)
а>0, значит ветви параболы направлены вверх и это значит, что функция положительна в интервале (-∞;-8)∪(3;+∞)
Находим вершину параболы:
х=-b/2a
x=-5/2=-2,5
(-2,5)²+5*(-2,5)-24=-30,25
Вершина (-2,5;-30,25)
По всем этим данным строим график.
1) Допустим, было 
граммов 5%-ой кислоты. Тогда, очевидно, 10%-ой было 
.
Составляем уравнение:
5% · + 10% ·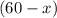 
= 8% · 60;
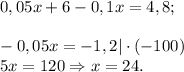
Тогда 5%-ого раствора было 24 г, а 10% - 60 - 24 = 36 (г).
ОТВЕТ: 5%-ого - 24 г, 10%-ого - 36 г.
2) Допусти, у нас есть "десятирублевок". Тогда "пятирублевок" всего 
.
Составляем уравнение:
Десятирублевых монет - 7. Пятирублевых - 25 - 7 = 18
ОТВЕТ: десятирублевых - 7; пятирублевых - 18.
3) Пусть вагон весит т. Тогда электровоз стоит 
.
Составляем уравнение:
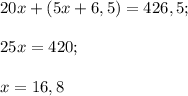
Один вагон весит 16,8 т. Тогда электровоз весит 5 · 16,8 + 6,5 = 90,5 (т).
ОТВЕТ: вагон весит 16,8 т, электровоз - 90,5 т.
Припустимо, що а, в – розміри ділянки.
Формули для периметра та площі прямокутника: Р = 2(a + в), S = а ∙ в. З іншої сторони Р = 40 м
2(а + в) = 40, а + в = 20
Нехай а = х, тоді в = 20 – х.
За змістом задачі число х задовольняє нерівність
0 < х < 20, тобто належить інтервалу (0; 20) .
Складаємо функцію:
S(x) = x(20 – x)
Функція S(x) неперервна на всій числовій прямій, тому будемо шукати її
найбільше і найменше значення на відрізку [0;20] .
Знаходимо критичні точки:
S '(x) = 20 – 2x; 20 – 2x = 0, x = 10
10 Є [0;20]
S(10) = 100; S(0) = 0; S(20) = 0
Найбільшого значення на відрізку [0;20] функція S набуває, якщо х = 10. Якщо
вона досягає найбільшого значення всередині відрізка [0;20], то вона набуває найбільшого значення і всередині інтервала (0, 20). Значить а = 10, тоді в = 20 – 10 = 10.
Отже, прямокутна ділянка буде мати найбільшу площу, якщо її розміри 10х10.
Відповідь: а = 10, в = 10
ответ: с графиком
Объяснение: