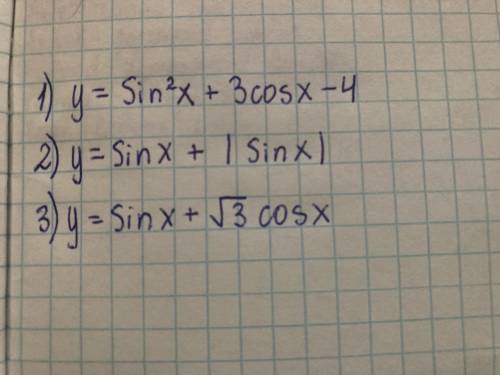
все таки математика настигла огромной волной и накрыла корнями и дробными степенями ???
(x)^1/n = ⁿ√x (например x^1/3 = ∛x x^1/2 = √x)
x² - y² = (x - y)(x + y)
(x + y)² = x² + 2xy + y²
(x^n)^m = x^(nn)
x^n * x^m = x^(n+m)
ⁿ√xⁿ = x (для положительных х)
x^-1 = 1/x
1. 64^1/6 = ⁶√(2⁶) = 2
2. 27 ^2/3 = ∛ 27² = ∛ (3³)² = 3² = 9
3. 0^51/4 = 0 (0 в любой положительной степени = 0)
5. x^1/2 = (x^1/4)²
(a^1/2 - b^1/2) / (a^1/4 + b^1/4) = (a^1/4 - b^1/4)(a^1/4 + b^1/4)/(a^1/4 + b^1/4) = a^1/4 - b^1/4
4. (x^1/3 + y^1/3)² - 2∛(xy) - 1/(∛y)^-2 = x^2/3 + 2x^1/3*y^1/3 + y^2/3 - 2x^1/3*y^1/3 - y^2/3 = x^2/3
^ - степень ( x^2/3 = ∛x² икс в степени две третьих)
Объяснение:
https://tex.z-dn.net/?f=%20%5Csqrt%7B11-4%20%5Csqrt%7B7%7D%7D%2B%20%5Csqrt%7B16-6%20%5Csqrt%7B7%7D%7D%3D%20%5Csqrt%7B7-2%2A2%20%5Csqrt%7B7%7D%2B4%7D%2B%5Csqrt%7B9-2%2A3%2A%5Csqrt%7B7%7D%2B7%7D%3D%20%5C%5C%20%3D%5Csqrt%7B%28%5Csqrt%7B7%7D%29%5E2-2%2A2%20%5Csqrt%7B7%7D%2B2%5E2%7D%2B%5Csqrt%7B3%5E2-2%2A3%2A%5Csqrt%7B7%7D%2B%28%5Csqrt%7B7%7D%29%5E2%7D%3D%20%5C%5C%20%3D%5Csqrt%7B%28%5Csqrt%7B7%7D-2%29%5E2%7D%2B%5Csqrt%7B%283-%20%5Csqrt%7B7%7D%29%5E2%7D%3D%7C%5Csqrt%7B7%7D-2%7C%2B%7C3-%20%5Csqrt%7B7%7D%7C%3D%20%5C%5C%20%3D%5Csqrt%7B7%7D-2%2B3-%20%5Csqrt%7B7%7D%3D1
Это ссылка!
1)
y = sin² x + 3 cos x - 4
y = 1 - cos²x + 3cos x - 4
y = -cos²x + 3cos x - 3
y' = 2cos x · sin x - 3sin x
y' = sin x · (2cos x - 3)
2cos x - 3 ∈ (-5; -1)
то есть 2cos x - 3 < 0
y' = 0
sin x = 0
точки экстремумов
х = 0; π; 2π; 3π или х = πn
При х = 0 + 2πn у = -1 + 3 - 3 = -1 - максимальное значение
При х = π + 2πn у = -1 - 3 - 3 = -7 - минимальное значение
у ∈ [-7; -1]
2)
y = sin x + |sin x|
sin x ∈ [-1; 1]
|sin x| ∈ [0; 1]
При х ∈ [0 + 2πn; π+2πn] y∈ [0; 2] половинки синусоид складываются
При х ∈ (π +2πn; 2π+2πn] y = 0 половинки синусоид взаимно уничтожаются
у ∈ [0; 2]
3)
y = sin x + √3 · cos x
y' = cos x - √3 · sin x
y' = 0
cos x = √3 · sin x
tg x = 1/√3
точки экстремумов
x = π/6; 7π/6; 13π/6; 19π/6 . . .
При х = π/6+ 2πn у = 0,5 + √3 · 0,5√3 = 2 (максимальное значение)
При х = 7π/6 + 2πn у = -0,5 - √3 · 0,5√3 = -2 (минимальное значение)
у ∈ [-2; 2]