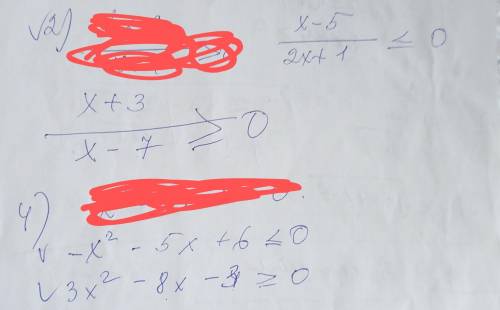
ответ: 1) 5х-у=1
х+3у=5
у=-1+5х
х+3(-1+5х)=5
решаем уравнение: х+3(-1+5х)=5
х-3+15х=5 - 16х-3=5
16х=5+3=8 - х=8|16 - х=1|2
возвращаемся к системе: у=-1+5х получаем у=-1+5*1|2
х=1|2 у=3|2
2) 9х+2у=16
3х-5у=11
х=16|9-2|9у
3(16|9-2|9e)-5у=11
решаем уравнение: 3(16|9-2|9e)-5у=11 16|3-2|3y-5y=11
16|3-17|3y=11 |умножаем на 3 (чтобы убрать дробь)
16-17y=33
-17у=33-16 -17у=17 у=-1
возвращаемся к системе: х=16|9-2|9у получаем х=16|9-2|9*(-1)
х=16|9+2|9 х=2
х=2 у=-1
3) 2х-3(2у+1)=15
3(х+1)=3у=2у-2
убираем в первом уравнении скобки: 2х-6у-3=15 2х=15+6у+3 2х=18+6у (делим на 2) х=9+3у
получаем: х=9+3у
3(9+3у+1)+3у=2у-2
Решаем уравнение: 3(9+3у+1)+3у=2у-2
3(10+3у)+3у=2у-2
30+9у+3у=2у-2 30+12у=2у-2
12у-2у=-2-30 10у=-32 (делим обе стороны на 10) у=-16|5
возвращаемся к системе: х=9+3у получаем х=9+3*(-16|5) получаем х=-3|5 y=-16|5
если стоит этот знак | - то это дробь
Так как каждый кубик может быть одного из двух цветов, то количевство возможных башен будет 2*2*2*2*2=32
А малышей 45, значит среди этих башен найдутся две одинаковые (32 разные, 33 -я по любому совпадет с одной из 32 башен)
Доказано
\\Обозначим цвета К и С
Тогда возможные варианты построения башень, начиная с нижнего
1
С
КККСК
ККСКК
КСККК
С
5
КККCC
ККССК
КССКК
ССККК
4
СКККС
СКСКК
СККСК
КСКСК
КСККС
ККСКС
6
СССКК
КСССК
ККССС
3
ССКСК
ССККС
КССКС
СКССК
СККСС
КСКСС
6
СКСКС
1
К
К
2
СССКС
СКССС
2
ССКСС
1
1
1+5+4+6+3+6+1+2+2+1+1=32 \\\
2)
2x ≠ -1 ⇒ x ≠ -0.5
x -5 = 0 ⇒ x = 5
Метод интервалов
+ - +
(- 0,5) [5]
x ∈ (-0.5; 5]
х ≠ 7
х + 3 = 0 ⇒ х = -3
Метод интервалов
+ - +
[- 3] (7)
x ∈ (-∞; -3]∪ (7; +∞)
4)
-x² - 5x + 6 ≤ 0
-x² - 5x + 6 = 0
D = 25 +24 = 49 = 7²
x₁ = -0.5 · (5 - 7) = 1
x₂ = -0.5 · (5 + 7) = -6
Метод интервалов
- + -
[- 6] [1]
x ∈ (-∞; -6] ∪ [1; + ∞)
3x² - 8x - 3 ≥ 0
3x² - 8x - 3 = 0
D = 64 +36 = 100 = 10²
x₁ = (8 - 10) : 6 = -1/3
x₂ = (8 + 10) : 6 = 3
Метод интервалов
+ - +
[- 1/3] [3]
x ∈ (-∞; -1/3] ∪ [3; + ∞)