а). В этом числе ноль встречается 9 раз, а числа 2, 3, 9 - по 20 раз.
б). Да, 123...9899 делится на 9.
Сначала посчитаем, сколько всего в числе 1234..9899 было выписано цифр 0, 1, 2, 3, 9. Это тоже самое, что и посчитать, сколько раз встречаются эти же цифры в числах от 1 до 99.
Цифра 0:
10, 20, 30, 40, 50, 60, 70, 80, 90 - всего 9 раз.
Цифра 1:
1, 10 - 19 (11 раз), 21, 31, 41, 51, 61, 71, 81 ,91 - всего 20 раз.
Понятно, что 2, 3, 9 встречаются столько же раз, сколько и 1 (все они могут стоять 10 раз в разряде единиц, и 10 раз - в разряде десятков).
Теперь нужно узнать, делится ли число 1234..9899 на 9.
Признак делимости на 9: число делится на 9 тогда и только тогда, когда сумма его цифр тоже делится на 9.Так что мы должны узнать, делится ли 1 + 2 + 3 + ... + 99 на 9.
Для этого найдем искомую сумму по формуле арифметической прогрессии:
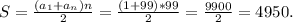
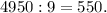
Так как получилось разделить нацело, то 1234...9899 делится на 9.
Відповідь:
Еще недавно, учась сложению чисел, мы складывали кучки из монет. Тогда перед нами стояла задачи сложить две кучки. Но допустим, мы хотим теперь сложить не две, а несколько кучек. Это можно было бы сделать так: сгребаем их все сразу в одну большую кучу и пересчитываем в ней все монеты. Такой сложения всем бы был хорош, да только ни на счетах, ни на бумаге нельзя сделать ничего подобного. На счетах и бумаге мы умеем складывать между собой только два числа. Поэтому мы не будем сгребать вместе сразу все кучки, а поступим так, чтобы все наши действия можно было легко перенести на бумагу.
Итак, перед нами несколько кучек из монет. Мы знаем, сколько монет в каждой кучке, и теперь мы хотим узнать, сколько же у нас всего монет во всех кучках. Мы берем любые две кучки и сдвигаем их вместе, образуя одну новую кучку побольше. Умея складывать два числа на бумаге, мы сможем легко вычислить, сколько у нас монет в новой кучке без фактического их пересчета. Теперь у нас стало на одну кучку меньше. Далее, берем еще две кучки, сливаем их воедино, вычисляем новое число монет в только что образованной кучке и, таким образом, снова уменьшаем количество кучек на одну. Мы повторяем и повторяем эту процедуру, уменьшая всякий раз число кучек на единицу, до тех пор пока у нас не останется одна-единственная большая куча. Число монет в этой куче нам известно, причем вычислили мы его на бумаге, а не прямым пересчетом.
Очевидно, мы получим один и тот же ответ, совершенно независимо от того, в каком порядке мы сдвигали кучки. А значит, когда перед нами находится сумма чисел, например,
8 + 9 + 2, мы можем вычислять ее тоже в любом порядке. Поэтому мы всегда будем выбирать такой порядок, какой для нас наиболее удобен. В данном случае удобно вначале сложить восьмерку и двойку, а потом добавить девятку:
8 + 2 + 9 = 10 + 9 = 19.
х- собственную скорость лодки
х-3 - скорость против течения
х+3 - скорость по течению
3(х-3) - расстояние против течения
2(х+3) - расстояние по течению
3(х-3)+2(х+3)=32
3х-9+2х+6=32
5х=35
х=7 км/ч - скорость лодки