ответ: доказано
Объяснение:
если через производную, то она равна -2х-16, находим критическую точку -2х-16=0, х=8
с неравенства 2х-16≥0 устанавливаем знак производной при переходе через критическую точку
-8
+ -
значит, функция возрастает на промежутке (-∞;-8] и убывает на промежутке [-8;+∞)
Кстати, этот же результат получим, решив вторым .
вершина параболы имеет абсциссу х₀=-b/2a=16/(-2)=-8, т.к. ее ветви направлены вниз, то функция возрастает на промежутке (-∞;-8] и убывает на промежутке [-8;+∞)
Возьмем две точки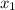 ,
, 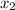 , причем
, причем 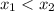 .
.
Им соответствуют значения функции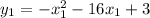 и
и 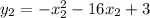 .
.
Сравним значения функций в данных точках. Для этого достаточно посмотреть на знак их разности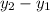 : если он положительный, то
: если он положительный, то 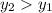 ; если равен нулю, то значения равны; иначе
; если равен нулю, то значения равны; иначе 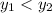 .
.
По предположению,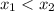 , поэтому вторая скобка отрицательна.
, поэтому вторая скобка отрицательна.
Если