Question

НОМЕР 0.9 применяя формулы сокращённого умножения, разложите многочлен на множители:
1) 4x²-9y²
2) -25a²+b²
3) 27x³-y³
4) 8a³+b³
5) 4m²-4mn+n²
6) 8xy+y²+16x²
7) m³+125
8)8a³-27b³
<3

Answer 1

Объяснение:

1)Применить формулу разности квадратов.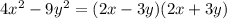 $4x^2 - 9y^2 = (2x - 3y)(2x+3y)\\$

2)Поменять местами первое и второе значения, далее применить формулу разности квадратов.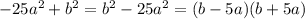 $-25a^2+b^2 = b^2 - 25a^2 = (b - 5a)(b + 5a)$

3)Разность кубов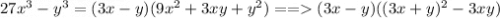$27x^3 - y^3 = (3x - y)(9x^2 + 3xy+ y^2) == (3x-y)((3x+y)^2-3xy)$

4)Сумма кубов: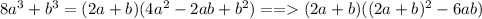$8a^3+b^3 = (2a + b)(4a^2 - 2ab + b^2) == (2a + b)((2a + b)^2 - 6ab)$

5)формула разности квадратов, только справа налево) 4m^2 - 4mn + n^2 = (2m - n)^2

6)тоже самое что и 5) только формула квадрата суммы: $8xy + y^2 + 16x^2 == 16x^2 + 8xy + y^2 == (4x + y)^2$

7)Сумма кубов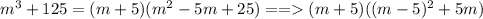$m^3 + 125 = (m + 5)(m^2 - 5m + 25) == (m + 5)((m - 5)^2 + 5m)$

8)Разность кубов: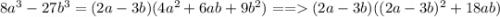 $8a^3-27b^3 = (2a - 3b)(4a^2 + 6ab + 9b^2) == (2a - 3b)((2a - 3b)^2 + 18ab)$

Надеюсь, что всё правильно.