
S1=80 cм2
S2=245 см2
Объяснение:
Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.
Коэффициент подобия k=4/7, но нам неизвестна площадь ни одного треугольника, а известна только сумма площадей S1+S2=325.
Обозначим:
S1 - площадь первого треугольника
325-S1=S2 - площадь второго треугольника
Составим отношение:
S1/(325-S1)=(4/7)^2
Возводим в квадрат дробь справа:
S1/(325-S1)=16/49
По правилу креста:
S1*49=16*(325-S1)
49*S1=5200-16*S1
49*S1+16*S1=5200
65*S1=5200
S1=5200:65
S1=80 cм2
Площадь второго треугольника 325-S1=325-80=245 см2
Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
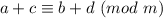
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
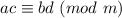
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
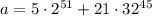
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например, 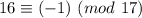 , но сейчас это не нужно), нам повезло, это 32
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что 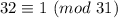 , получаем
, получаем
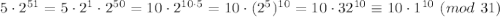
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
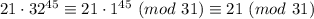
Остаток 21, чудесно. Выполняем последний шаг.
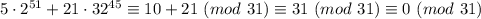
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
Объяснение:
1.
а)
б)
в)
г)
2.