а)
т.к график проходит через начало отсчёта, то он график прямой пропорциональности вида: y=kx
Найдём точку, лежащую на графике с координатами (2;1). x=2, y=1
1=k×2
k=1:2
k=0,5
Этот график: y=0,5x
б)
График не проходит через начало отсчёта и он паралеллен оси абсцисс.
Следовательно:
Этот график вида: y=b, где b-некоторое число.
Судя по графику b=2.
Этот график: y=2
в)
График не проходит через начало отсчёта и он не паралеллен одной из осей. Следовательно он вида: y=kx+b
Точки пересечения: (0;3) и (2;0)
Подставим и получим:
3=k×0+b
0=k×2+b
Заметим, что в первом уравнении b=3. т.к k обратится в ноль.
Запишем в новом виде второе уравнение и получим:
0=k×2+3
2k=-3
k=-3:2
k=-1,5
Нашли все неизвестные переменные и уже, наконец, уравнение этого графика: y=-1,5x+3
ОДЗ: х принадлежит (-бесконечность; -4) U (4; +бесконечность)
для нахождения экстремума нужно найти производную...
f ' (x) = ((2x-5)(x+4) - (x^2-5x)) / (x+4)^2 = (2x^2 + 3x - 20 - x^2 + 5x) / (x+4)^2 =
= (x^2 + 8x - 20) / (x+4)^2 = (x-2)(x+10) / (x+4)^2
решение неравенства (x-2)(x+10) / (x+4)^2 > 0 (корни: -10; -4; 2)
х принадлежит (-бесконечность; -10) U (2; +бесконечность) =>
функция возрастает при х принадлежит (-бесконечность; -10] U [2; +бесконечность)
функция убывает при х принадлежит [-10; -4) U (-4; 2]
при х = -10 ---функция достигает максимума fmax = (100+50)/(-6) = -25
при х = 2 ---функция достигает минимума fmin = (4-10)/6 = -1
система:
9x - x^2 > 0
5 - x > 0
lg(5-x) не равен 0
x(9 - x) > 0
x < 5
5 - x не равно 1
х принадлежит (-бесконечность; 0) U (9; +бесконечность)
х принадлежит (-бесконечность; 5)
х не равен 4
х принадлежит (-бесконечность; 0) --- x < 0
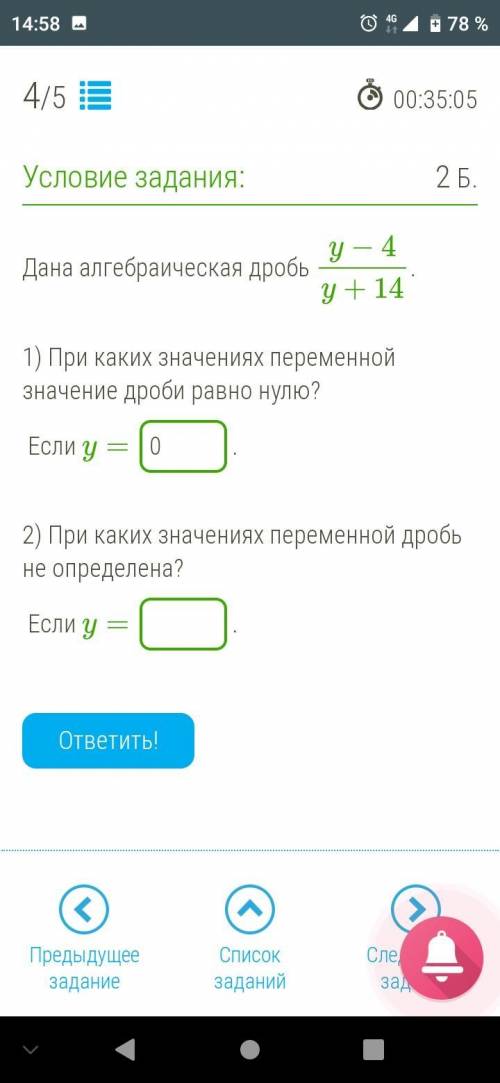
1) y = 4
2) y = -14
Объяснение:
1) Значение дроби равно нулю, если её числитель равен 0, т.е. y - 4 = 0 ⇒ y = 4
2) Дробь не определена, если её знаменатель равен 0, т.к. на 0 делить нельзя, т.е. y + 14 = 0 ⇒ y = -14