1) a) 4+12x+9x2
4+12x+18
22+12x
2(11+6x)
б) 25-40х+16х2
25-40х+32
57-40х
г) -56а+49а*2+16
-56а+98а+16
42а+16
2(21а+8)
2) a) (y-1)(y+1) б) p^2-9 г) (3x-2)(3x+2) д) (3x)^2-2^2 е) a^2-3^2
y^2-1 (3x)^2-2^2 9x^2-4 a^2-9
в) 4^2-(5y^2) 9x^2-4
16-25y^2
4) a) a3-b3 б) 27a3+8b3
3(a-b) 81a+24b
3(27a+8b)
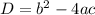(если дискриминант больше нуля уравнение имеет 2 корня, если равен нулю, уравнение имеет 1 корень, если меньше нуля, то нет корней), либо применяя разложение многочлена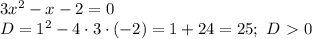
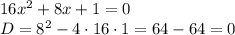
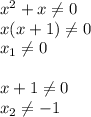
решение на листочке...