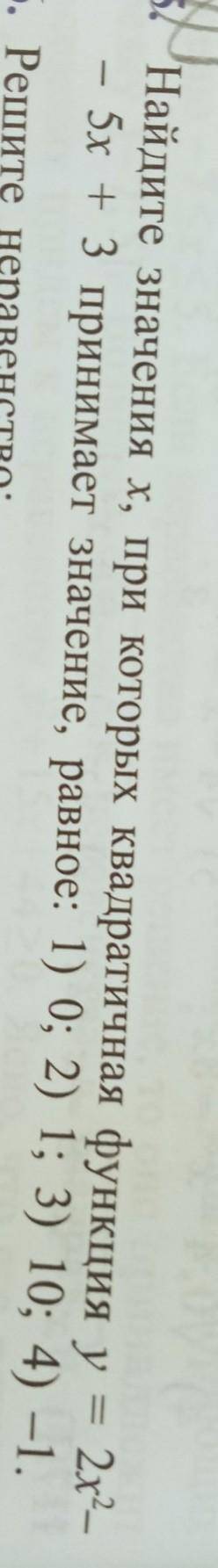
Если P(x) делится на Q(x), то
P(x)/Q(x)=A(x) ,где A(x)-многочлен.
Поскольку Q(x) делится на P(x),то
Q(x)/P(x)=B(x) ,где B(x) -многочлен.
Откуда верно, что:
A(x)*B(x)=1
Если знаете комплексный анализ, то очевидно, что многочлен со степенью больше нуля имеет хотя бы один корень (комплексный или действительный),но тогда и произведение многочленов должно иметь этот корень,но многочлен C(x)=A(x)*B(x)=1 ,не может иметь корней тк 1 не равно 0.
А значит оба многочлена A(x) и B(x) имеют нулевую степень (константы),таким образом B(x)=c.(с не равно 0)
Q(x)=c*P(x)
Пусть многочлен A(x) имеет степень n ,а многочлен B(x) имеет степень m.Тогда очевидно, что многочлен A(x)*B(x) имеет степень m+n, но 1 это многочлен нулевой степени:
m+n=0
Тк m>=0 и n>=0, то m=n=0.
То есть B(x)=c (с не равно 0)
Q(x)=c*P(x) ,что и требовалось доказать.
27 минут =27/60 часа=9/20 часа
29 минут =29/60 часа
время, которое велосипедит тратит на прохождение пути s/v
Если он увеличит скорость на 9км/ч , то время прохождения станет s/(v+9)
s/v - s/(v+9) = 9/20
Если он уменьшит скорость на 5км/ч , то время прохождения станет s/(v-5)
s/(v-5) - s/v = 29/60
получили систему из двух уравнений. Выразим s из каждого из них
первое уравнение
s/v - s/(v+9) = 9/20
s(1/v - 1/(v+9)) = 9/20
s((v+9-v)/v(v+9)) = 9/20
s(9/v(v+9)) = 9/20
s(1/v(v+9)) = 1/20
s=v(v+9)/20
второе уравнение
s/(v-5) - s/v = 29/60
s(1/(v-5) - 1/v) = 29/60
s((v-(v-5))/v(v-5) ) = 29/60
s(5)/v(v-5) ) = 29/60
s=29v(v-5)/300
теперь приравняем оба уравнения
v(v+9)/20=29v(v-5)/300
(v+9)/2=29(v-5)/30
15(v+9)=29(v-5)
15v+135=29v-145
14v=280
v=20 км/ч