Пусть v катера будет х, а v течения реки будет у. Если катер часа по течению, то за это время он расстояние: (х+у)3. Когда он проходил по озеру, то находился в стоячей воде без течения и расстояние 3х. За 6 часов он расстояние 114км, и теперь составим уравнение:
(х+у)3+3х=114. Разберём вторую часть задачи. Катер против течения 4 часа, поэтому за это время он х-у)4. Так как он расстояние на 10 км больше, чем за 3 часа по озеру, то по озеру он пройдёт 2х и разница составляет 10км. По этим данным составим второе уравнение:
(х-у)4-3х=10. Решим систему уравнений:
{(х+у)3+3х=114
{(х-у)4-3х=10
{3х+3у+3х=114
{4х-4у-3х=10
{6х+3у=114 |÷3
{х-4у=10
{2х+у=38
{х=10+4у.
Подставим эти значения в первое уравнение:
2х+у=38
2(10+4у)+у=38
20+8у+у=38
9у=38-20
9у=18
у=18÷9
у=2; итак v течения реки=2км/ч
Теперь подставим в уравнение значение у:
х=10+4у
х=10+4×2=10+8=18км/ч.
ответ: v катера=18км/ч;
v течения реки=2км/ч
1)
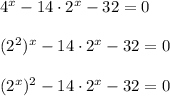
Введём замену: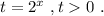 
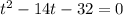
По теореме Виета:
.
Но так как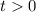 
, то -2 не является решением этого уравнения. Выполняем обратную замену:
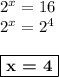
ответ: 4.
2)
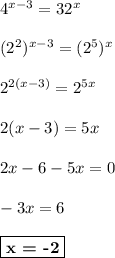
ответ: -2.
3)
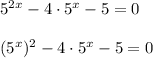
Введём замену: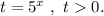 
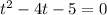
По теореме Виета:
Но так как 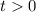, то -1 не является решением этого уравнения. Выполняем обратную замену:
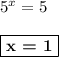
ответ: 1.
4)
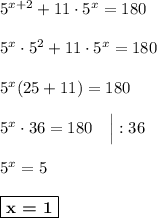
ответ: 1.
5)
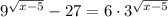
Для начала кое-что учтём: подкоренное выражение всегда неотрицательно. То есть:
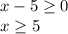
Продолжаем решение:
Введём замену: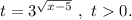 
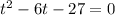
По теореме Виета:
Но так как 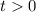, то -3 не является решением этого уравнения. Выполняем обратную замену:
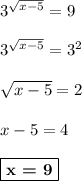
ответ: 9.
a) если n =3 корней нет
б)(n-3)X=6
если икс равен 3 то n =5