Question

Решите два логарифмических уравнения.

Answer 1

1) $\log_5x+\log_x5=2;\ x0;\ x\not= 1;\ \log_5x+\dfrac{1}{\log_5x}=2;\ \log_5x=t;$

$t+\dfrac{1}{t}=2;\ \dfrac{t^2-2t+1}{t}=0;\ (t-1)^2=0;\ t=1;\ x=5.$

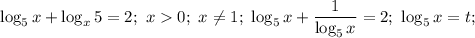
Проверка: 1+1=2 - верно.

ответ: 5

2) $x^{\log_36}+6^{\log_3x}=12;\ 6^{\log_3x}+6^{\log_3x}=12;\ 6^{\log_3x}=6^1;\ \log_3x=1; x=3.$

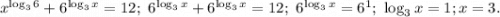
ответ: 3

Мы воспользовались формулой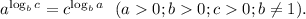 $a^{\log_bc}=c^{\log_ba}\ \ (a0; b0; c0; b\not=1).$

Ее можно доказать, прологарифмировав левую и правую части по основанию b.