Координаты точки пересечения прямых (3; -1)
Решение системы уравнений (3; -1)
Объяснение:
Решить графически:
у=х-4
у= -х/3
Построить графики. Графики линейной функции, прямые линии. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
у=х-4 у= -х/3
Таблицы:
х -1 0 1 х -3 0 3
у -5 -4 -3 у 1 0 -1
Согласно графика, координаты точки пересечения прямых (3; -1)
Решение системы уравнений (3; -1)
прощения, что не в рукописном варианте, но думаю, что ход мыслей будет понятен=)
Нужно помнить, про то, что значение x, стоящего под логарифмом - всегда строго больше нуля (ОДЗ: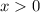 
).
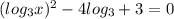
Пусть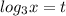 
, тогда:
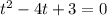
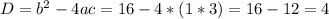
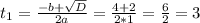
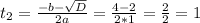
Тогда:
1). 
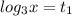
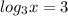(теперь нужно представить 3 так, чтобы под логарифмом было такое число, которое с основанием логарифма 
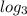будет равняться 3 (иначе говоря 3 в степени 3 (первая 3 - для того, чтобы сократить 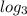и после этого осталась чистая степень - 3)
(таким числом под логарифмом будет 27: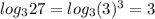 
)
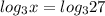(одинаковые логарифмы с основанием 3>1 - можем их убрать)
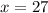
2). 
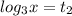
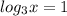(сделаем тоже самое: нужно представить 1 так, чтобы под логарифмом было такое число, которое с основанием логарифма 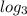будет равняться 1 (иначе говоря 3 в степени 1 (3 - для того, чтобы сократить 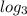и после этого осталась чистая степень - 1))
(таким числом под логарифмом будет 3: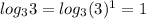 
)
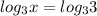(одинаковые логарифмы с основанием 3>1 - можем их убрать)
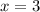
ответ: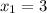 
, 
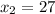
а) область определения функции;
D = ( -∞ ; +∞ )
б) область значений функции;
E = ( -∞ ; +∞ )
в) промежутки возрастания функции;
( -∞ ; -1 ) ∪ ( 1 ; +∞ )
г) промежутки убывания функции;
( -1 ; 1 )
д) нули функции;
f = 0 ⇔ x ∈ { -1,75 ; 1,75 ; 0 }
е) промежутки на которых функция принимает положительные значения;
f > 0 ⇔ x ∈ (-1,75 ; 0) ∪ (1,75 ; +∞ )
ж) промежутки на которых функция принимает отрицательные значения.
f < 0 ⇔ x ∈ ( -∞ ; -1,75) ∪ ( 0 ; 1,75 )
Объяснение
Надеюсь вовремя