ответ: При діленні сумми цих двох чисел на 11 отримаєм завжди число рівне суммі двох цифер з яких складаються данні числа.
Объяснение: Позначемо двоцифрове число (ab). Де а і b - довільні натуральні числа. Зворотнє двоцифрове число буде мати вигляд: (ba).
Розпишем двоцифрове число (ab) : ab=10×a +b;
Розпишем зворотнє двоцифрове число (ba) : ba=10×b+a;
Тепер запишем сумму цих чисел: ab + ba=(10×a+b) + (10×b+a)=
=10a+b+10b+a=11a+11b=11×(a+b).
Отримана сумма (11×(а+b))/11=(a+b), при діленні на 11 завжди буде рівна суммі цих цифр (a+b) з яких складаються ці числа, при любих
довільних а і b.
Наприклад: 13+31=44;
44/11=4;
Тут а=1, b=3, (a+b)=1+3=4.
1.
a)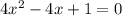
б)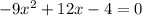
в)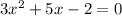
2.
a)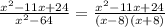
б)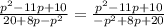
3.