Объяснение:
1) 5x/x+1 - x-4/x+1=0. Умножим всё на знаменатель дроби. Тогда будет: 5х-х-4=0. Решаем его: 4х=4. Здесь нужно разделить на число около х: х=1
2) 3-2x/x^2-25 - 8-x/x^2-25 =0. Тоже умножаем на знаменатель:3-2х-8-х=0. Решаем получившееся уравнение.
-3х=-3+8. Здесь меняются знаки, потому что мы переносим из одной части в другую.
-3х=5. Делим на число у х.
Х=-5/3. Можно выделить целую часть. Х=-1 целая 2/3.
3)y^2-8y/y-3 - 9+2y/3-y =0. У нас похожие значения в знаменатели. Делаем их одинаковыми: y^2-8y/y-3+9-2у/у-3=0. Теперь делим на знаменатель: у^2-8у+9-2у=0. Сложим подобные слагаемые:
У^2-10у+9=0. Это квадратное уравнение. Его надо решить с дискиименанта.
Дискиименант=b^2-4ac=(-10)^2-4*1*9=100-36=64=8^2
У1,2= -b+/- корень из дискрименанта/2а.
У1,2=10+/-8/2 У1=10+8/2= 18:2=9.
У2=10-8/2=2/2=1. ответ: у1=9, у2=1.
Прости, я знаю только эти три.
Простыми преобразованиями эту задачу не решить, будем использовать арифметику остатков.
1-ое свойство, которое понадобится
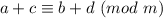
То есть мы спокойно можем заменить каждое слагаемое сравнимым с ним по модулю m. То есть каждое слагаемое в нашей сумме будем рассматривать отдельно.
2-ое свойство, которое нам понадобится:
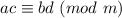
То есть довольно аналогичная вещь в произведении
На нашем примере все увидим
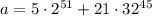
Находим остатки по модулю 31
Рассматриваем первое слагаемое. Просто двойка не годится, нам нужно найти ближайшее к 31 число, превосходящее его (иногда там в отрицательные числа залезаем, например, 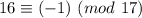 , но сейчас это не нужно), нам повезло, это 32
, но сейчас это не нужно), нам повезло, это 32
Учитываем, что 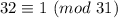 , получаем
, получаем
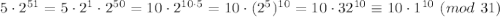
То есть остаток от деления первого слагаемое на 31 получился равным 10. Прекрасно, аналогично со вторым
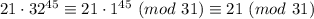
Остаток 21, чудесно. Выполняем последний шаг.
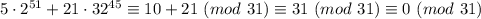
То есть остаток от деления исходного числа на 31 равен 0, следовательно, исходное число делится на 31, что и требовалось доказать.
Решение задачи.
1. Обозначим через х количество компьютеров на первом складе.
2. Найдем количество компьютеров на втором складе.
2х.
3. Найдем количество компьютеров на третьем складе.
3х.
4. Сколько компьютеров стало на первом складе?
х - 7.
5. Сколько компьютеров стало на третьем складе?
3х - 16.
6. Сколько компьютеров стало на втором складе?
2х + 17.
7. Сколько компьютеров стало на первом и третьем складе вместе?
х - 7 + (3х - 16) = 4х - 23.
8. Составим и решим уравнение.
2х + 17 = 4х - 23;
2х = 40;
х = 20.
9. Первоначальное количество компьютеров на первом складе равно х =20.
10. Сколько компьютеров было на втором складе?
20 * 2 = 40.
11. Сколько компьютеров было на третьем складе?
20 * 3 = 60.
ответ. На первом складе было 20 компьютеров, на втором складе 40 компьютеров, на третьем складе 60 компьютеров.
решение на фотографии
Объяснение:
решил только 3(