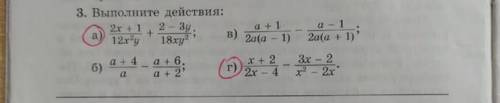
ответ: 50 м и 60 м
Объяснение: Пусть длина участка x м, а ширина - y м, тогда площадь участка равна xy, а периметр равен 2·(x + y).
Составим систему уравнений:
xy = 3000
2x + 2y = 220
Второе уравнение разделим на 2:
xy = 3000
x + y = 110
Решим систему подстановки:
xy = 3000
x = 110 - y
(110 - y)·y = 3000
110y - y² = 3000
-y² + 110y - 3000 = 0
y² - 110y + 3000 =0
D = b² - 4ac = (-110)² - 4·3000 = 12100 - 12000 = 100
x₁ = 110 + √100 / 2 = 110 +10 / 2 = 60
x₂ = 110 - 10 / 2 = 50
y₁ = 110 - 60 = 50
y₂ = 110 - 50 = 60
Решением системы являются две пары чисел (60; 50) и (50; 60). Следовательно, стороны прямоугольника равны 50м и 60м.
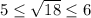
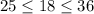
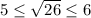. Возведя все части неравенства в квадрат, получим 
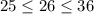. Неравенства выполняются, следовательно, число √26 заключен между числа 5 и 6.
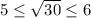. Возведя все части неравенства в квадрат, получим: 
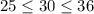. Видим, что неравенства правильны, следовательно, число √30 заключен между числа 5 и 6.
3х^2 + у^2 - ху = 3
2х^2 - 4у^2 + 3ху = 1
Умножаем на 3 второе уравнение
6х^2 - 12у^2 + 9ху = 3
Вычитаем из результата первое уравнение
3х^2 - 13у^2 + 10ху = 0
3х^2 + 10ху - 13у^2 = 0
(3x+13y)(x-y) = 0
1 Вариант x=y
3х^2 + x^2 - хx = 3
х^2 = 1
x₁=1. y₁=1
x₂=-1, y₂=-1
2 Вариант x = -(13/3)y
3( -13/3y)^2 + у^2 - ( -13/3y)y = 3
169/3y^2+y^2+13/3y^2 = 3
169y^2+3y^2+13y^2 = 9
185y^2 = 9
y₁ = 3/√185, x₁= -(13/3)(3/√185) = -13/√185
y₂ = -3/√185, x₂= -(13/3)(-3/√185) = 13/√185