На доске написано 2021 натуральное число, причём для любых 1010 написанных чисел среди остальных найдётся число, взаимно простое с каждым из них. Докажите, что есть написанное число, взаимно простое с каждым из остальных.
Если функция y = f(x) непрерывна на отрезке [a, b], то она достигает на этом отрезке наименьшего и наибольшего значений. Это, как уже говорилось, может произойти либо в точках экстремума, либо на концах отрезка. Поэтому для нахождения наименьшего и наибольшего значений функции, непрерывной на отрезке [a, b], нужно вычислить её значения во всех критических точках и на концах отрезка, а затем выбрать из них наименьшее и наибольшее.
Пусть, например, требуется определить наибольшее значение функции f(x) на отрезке [a, b]. Для этого следует найти все её критические точки, лежащие на [a, b].
1)
ОДЗ: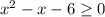
⇒ 
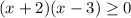⇒ ![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
два корня
или 
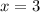
C учетом![x \in (-\infty; -2] \cup [3;+\infty)](/tpl/images/1361/5355/f678f.png)
получаем ответ:
2)
ОДЗ: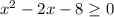
⇒ 
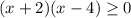⇒ ![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
два корня
или 
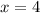
C учетом![x \in (-\infty; -2] \cup [4;+\infty)](/tpl/images/1361/5355/4ed2b.png)
получаем ответ:
3)
Так как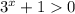
при любых х, возводим данное неравенство в квадрат:
D=16-12=4
Показательная функция с основанием 3 возрастает
О т в е т. (0;1)
4)
Так как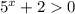
при любых х, возводим данное неравенство в квадрат:
D=36-20=16
Показательная функция с основанием 5 возрастает
О т в е т. (0;1)